第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
8.如图,$P$为$\triangle ABC$内一点,$\angle BAC=70^{\circ}$,$\angle BPC=120^{\circ}$,$BD$是$\angle ABP$的平分线,$CE$是$\angle ACP$的平分线,$BD$与$CE$交于点$F$,则$\angle BFC=$
(
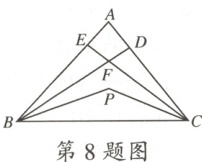
A.$85^{\circ}$
B.$90^{\circ}$
C.$95^{\circ}$
D.$100^{\circ}$
(
C
)
A.$85^{\circ}$
B.$90^{\circ}$
C.$95^{\circ}$
D.$100^{\circ}$
答案:
8.C [解析]
∵∠BAC = 70°,
∴∠ABC + ∠ACB = 180° - ∠BAC = 110°.
∵∠BPC = 120°,
∴∠PBC + ∠PCB = 180° - ∠BPC = 60°,
∴∠ABP + ∠ACP = 110° - 60° = 50°.
∵BD是∠ABP的平分线,CE是∠ACP的平分线,
∴∠FBP + ∠FCP = 25°,
∴∠FBC + ∠FCB = ∠PBC + ∠PCB + ∠FBP + ∠FCP = 85°,
∴∠BFC = 180° - (∠FBC + ∠FCB) = 95°.故选C.
∵∠BAC = 70°,
∴∠ABC + ∠ACB = 180° - ∠BAC = 110°.
∵∠BPC = 120°,
∴∠PBC + ∠PCB = 180° - ∠BPC = 60°,
∴∠ABP + ∠ACP = 110° - 60° = 50°.
∵BD是∠ABP的平分线,CE是∠ACP的平分线,
∴∠FBP + ∠FCP = 25°,
∴∠FBC + ∠FCB = ∠PBC + ∠PCB + ∠FBP + ∠FCP = 85°,
∴∠BFC = 180° - (∠FBC + ∠FCB) = 95°.故选C.
9.(灵宝期中)如图,在$\triangle ABC$中,$AD$为中线,$DE$和$DF$分别为$\triangle ADB$和$\triangle ADC$的高.若$AB=3$,$AC=4$,$DF=1.5$,则$DE=$

2
.
答案:
9.2
10.一副直角三角板按如图所示放置,其中$\angle C=\angle DFE=90^{\circ}$,$\angle A=45^{\circ}$,$\angle E=60^{\circ}$,点$F$在$CB$的延长线上,点$D$在$AC$上,$AB$与$DF$相交于点$O$.若$DE// CF$,则$\angle BOF=$

15°
.
答案:
10.15°
11.已知一张三角形纸片$ABC$(如图甲),其中$\angle ABC=\angle C$.将纸片沿过点$B$的直线折叠,使点$C$落到$AB$边上的点$E$处,折痕为$BD$(如图乙).再将纸片沿过点$E$的直线折叠,点$A$恰好与点$D$重合,折痕为$EF$(如图丙).原三角形纸片$ABC$中,$\angle ABC=$

72°
.
答案:
11.72° [解析]设∠ABC = ∠C = 2α,则∠A = 180° - ∠ABC - ∠C = 180° - 4α.由折叠得∠BED = ∠C = 2α,∠ADE = ∠A = 180° - 4α.
∵∠BED是△AED的外角,
∴∠BED = ∠A + ∠ADE,
∴2α = 180° - 4α + 180° - 4α,解得α = 36°,
∴∠ABC = 72°.
∵∠BED是△AED的外角,
∴∠BED = ∠A + ∠ADE,
∴2α = 180° - 4α + 180° - 4α,解得α = 36°,
∴∠ABC = 72°.
12.(禹州期中)下列说法正确的是 (
A.周长相等的两个图形一定是全等图形
B.两个正方形一定是全等图形
C.形状相同的两个图形一定是全等图形
D.两个全等图形的面积一定相等
D
)A.周长相等的两个图形一定是全等图形
B.两个正方形一定是全等图形
C.形状相同的两个图形一定是全等图形
D.两个全等图形的面积一定相等
答案:
12.D
13.如图,$\triangle ABC\cong\triangle AED$,点$E$在线段$BC$上,$\angle1=56^{\circ}$,则$\angle BAE$的度数为 (

A.$34^{\circ}$
B.$56^{\circ}$
C.$62^{\circ}$
D.$68^{\circ}$
B
)
A.$34^{\circ}$
B.$56^{\circ}$
C.$62^{\circ}$
D.$68^{\circ}$
答案:
13.B
14.如图,在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,以顶点$A$为圆心,适当长为半径画弧,分别交$AB$,$AC$于点$D$,$E$,再分别以点$D$,$E$为圆心,大于$\frac{1}{2}DE$长为半径画弧,两弧交于点$F$,作射线$AF$交边$BC$于点$G$.连接$BE$,则下列结论错误的是 (

A.$AE=CE$
B.$\angle A=\angle D$
C.$\angle EBC=45^{\circ}$
D.$AB\bot DF$
D
)
A.$AE=CE$
B.$\angle A=\angle D$
C.$\angle EBC=45^{\circ}$
D.$AB\bot DF$
答案:
14.D
查看更多完整答案,请扫码查看


