第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
15.(名师原创)如图,在$\triangle ABC$中,$AC\bot BC$,延长$BC$到点$D$,使$CD=AC$.$E$为$AC$上一点,且$DE=AB$,延长$DE$交$AB$于点$F$,连接$BE$,则下列结论错误的是 (
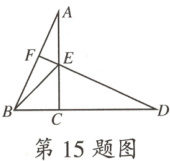
A.$AE=CE$
B.$\angle A=\angle D$
C.$\angle EBC=45^{\circ}$
D.$AB\bot DF$
A
)
A.$AE=CE$
B.$\angle A=\angle D$
C.$\angle EBC=45^{\circ}$
D.$AB\bot DF$
答案:
15.A
16.如图,在四边形$ABCD$中,$AC$平分$\angle BAD$,$AD=AC$,在$AC$上截取$AE=AB$,连接$DE$,$BE$,并延长$BE$交$CD$于点$F$.有以下结论:①$\triangle BAC\cong\triangle EAD$;②$\angle ABE+\angle ADE=\angle BCD$;③$BC+CF=DE+EF$.其中正确的个数是 (
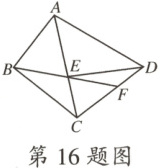
A.$0$
B.$1$
C.$2$
D.$3$
D
)
A.$0$
B.$1$
C.$2$
D.$3$
答案:
16.D [解析]
∵AC平分∠BAD,
∴∠BAC = ∠EAD,又
∵AB = AE,AC = AD,
∴△BAC ≌ △EAD,故①正确;
∴∠ACB = ∠ADE,BC = DE,
∵AB = AE,AC = AD,
∴∠ABE = ∠AEB,∠ACD = ∠ADC,又∠BAE = ∠CAD,
∴∠ABE = ∠ACD,
∴∠ABE + ∠ADE = ∠ACD + ∠ACB = ∠BCD,故②正确;
∵∠CEF = ∠AEB,∠ABE = ∠AEB,∠ABE = ∠ACD,
∴∠CEF = ∠ECF,
∴EF = CF,
∴BC + CF = DE + EF,故③正确.综上所述,结论正确的个数是3.故选D.
∵AC平分∠BAD,
∴∠BAC = ∠EAD,又
∵AB = AE,AC = AD,
∴△BAC ≌ △EAD,故①正确;
∴∠ACB = ∠ADE,BC = DE,
∵AB = AE,AC = AD,
∴∠ABE = ∠AEB,∠ACD = ∠ADC,又∠BAE = ∠CAD,
∴∠ABE = ∠ACD,
∴∠ABE + ∠ADE = ∠ACD + ∠ACB = ∠BCD,故②正确;
∵∠CEF = ∠AEB,∠ABE = ∠AEB,∠ABE = ∠ACD,
∴∠CEF = ∠ECF,
∴EF = CF,
∴BC + CF = DE + EF,故③正确.综上所述,结论正确的个数是3.故选D.
17.为了庆祝神舟二十号的成功发射,学校组织了一次小制作展示活动,小明计划制作一个如图所示的简易模型,已知该模型满足$\triangle ABD\cong\triangle ACE$,点$B$和点$C$是对应顶点,若$AB=8$cm,$AD=3$cm,则$DC=$
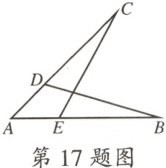
5
cm.
答案:
17.5
18.如图,在$\triangle ABC$中,$AB=CB$,$\angle ABC=90^{\circ}$,$AD\bot BD$于点$D$,$CE\bot BD$于点$E$.若$AD=5$,$CE=7$,则$DE$的长为
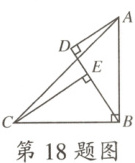
2
.
答案:
18.2
19.如图,$\angle1=\angle2$,$AE=AC$,要使$\triangle ADE\cong\triangle ABC$,则可添加的一个条件是
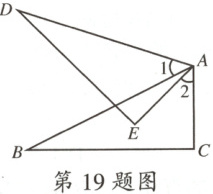
AD = AB(答案不唯一)
.(写出一个即可)
答案:
19.AD = AB(答案不唯一)
20.(邓州期中)如图,在$2×2$的正方形网格中,线段$AB$,$CD$的端点均在格点上,则$\angle1+\angle2=$
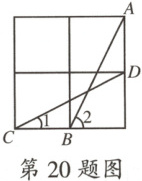
90°
.
答案:
20.90°
21.(兰考期末)如图,在$\triangle ABC$中,点$A$的坐标为$(0,1)$,点$C$的坐标为$(4,3)$,如果要使$\triangle ABD$与$\triangle ABC$全等(点$D$不与点$C$重合),那么点$D$的坐标是
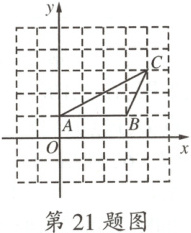
(4, - 1)或( - 1,3)或( - 1, - 1)
.
答案:
21.(4, - 1)或( - 1,3)或( - 1, - 1) [解析]如图,满足条件的点D有三个,点D₁的坐标是(4, - 1),点D₂的坐标是( - 1,3),点D₃的坐标是( - 1, - 1).
21.(4, - 1)或( - 1,3)或( - 1, - 1) [解析]如图,满足条件的点D有三个,点D₁的坐标是(4, - 1),点D₂的坐标是( - 1,3),点D₃的坐标是( - 1, - 1).

22.围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是轴对称图形的是 ( )
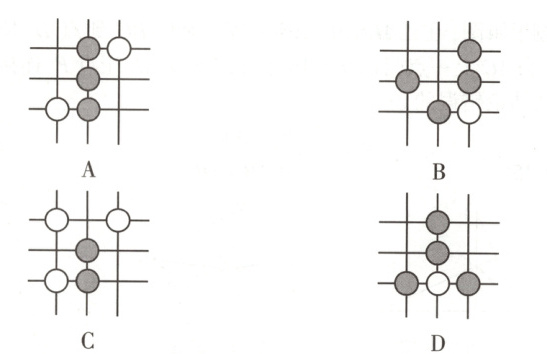

答案:
22.D
查看更多完整答案,请扫码查看


