《2025年昕金立文化单元金卷八年级数学上册人教版》

13.若一个整数能表示成$a^2 + b^2$(a,b 为整数)的形式,则称这个数为“完美数”.例如:$5 = 2^2 + 1^2$,则 5 是一个完美数.已知$M = x^2 + 4y^2 + 4x - 12y + k$(x,y 是整数,k 是常数),要使 M 为“完美数”,则 k 的值为13.

答案： 13

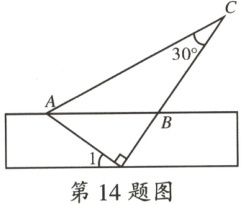
14.将一个三角尺和一把直尺按如图所示的方式摆放.若△ABC 是等腰三角形,则$∠1$的度数是30°.
!img !img

答案： 30°

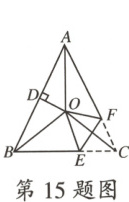
15.如图,在△ABC 中,$AB = AC$,$∠BAC = 48^{\circ}$,∠BAC 的平分线与线段 AB 的垂直平分线 OD 交于点 O.连接 OB,OC,将$∠ACB$沿 EF(点 E 在 BC 上,点 F 在 AC 上)折叠,点 C 与点 O 恰好重合,则$∠OEC =$96°.

答案： 96° 【解析】$\because \angle BAC=48°$，$AO$为$\angle BAC$的平分线，$\therefore \angle BAO=\angle CAO=\frac{1}{2}\angle BAC=24°.\because AB=AC,\therefore \angle ABC=\frac{1}{2}(180°-\angle BAC)=66°.\because OD$是$AB$的垂直平分线，$\therefore OA=OB,\therefore \angle ABO=\angle BAO=24°,\therefore \angle OBC=\angle ABC-\angle ABO=42°.\because OA=OA$，$\angle BAO=\angle CAO$，$AB=AC$，$\therefore \triangle AOB\cong\triangle AOC$，$\therefore OB=OC$，$\therefore \angle OCB=\angle OBC=42°.$由折叠可知$OE=CE$，$\therefore \angle COE=\angle OCB=42°.$在$\triangle OCE$中，$\angle OEC=180°-\angle COE-\angle OCB=96°.$

16.(8 分)计算:
(1)$(15x^2y - 10xy^2) ÷ 5xy$;
(2)$(2x - 1)^2 - (2x + 5)(2x - 5)$;
(3)$(a - 2b + 1)(a + 2b + 1)$;
(4)$(x + 2y - 1)^2$.

答案： 解:
(1)原式$=15x^{2}y÷5xy-10xy^{2}÷5xy =3x - 2y$.
(2)原式$=4x^{2}-4x + 1-(4x^{2}-25)=4x^{2}-4x + 1-4x^{2}+25=-4x + 26$.
(3)原式$=(a + 1)^{2}-(2b)^{2}=a^{2}+2a + 1-4b^{2}$.
(4)原式$=[(x + 2y)-1]^{2}=(x + 2y)^{2}-2(x + 2y)+1=x^{2}+4y^{2}+4xy-2x-4y + 1$.