《2025年昕金立文化单元金卷八年级数学上册人教版》

14.如图，在Rt△ABC中，∠A=90°，∠B=30°，CM平分∠ACB交AB于点M，过点M作MN//BC交AC于点N.若AN=1，则BC的长为6.

答案： 14.6

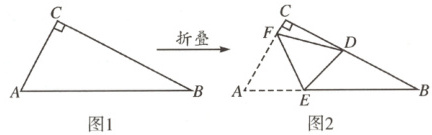
15.如图1，在△ABC中，∠ACB=90°，AC＜BC，将△ABC沿EF折叠，使点A落在直角边BC上的点D处.如图2所示，设EF与AB，AC边分别交于点E，F.如果折叠后△CDF与△BDE均为等腰三角形，那么∠B=30°.

答案：
15.30° 【解析】
∵在△CDF 中,∠C=90°,
∴若△CDF 是等腰三角形,则 CF=CD,
∴∠CFD=∠CDF=45°.连接 AD.设∠DAE=x,由折叠可知,AF=FD,AE=DE,
∴∠FDA=$\frac{1}{2}$∠CFD=22.5°,∠DEB=2x.分三种情况:①当 DE=DB 时,如图1,则∠B=∠DEB=2x,由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,解得 x=22.5°,则∠B=2x=45°.
∵AC＜BC,
∴∠B=45°不成立;②当 BD=BE 时,如图2,则∠B=180° - 4x.由∠CDE=∠DEB+∠B,得45°+22.5°+x=2x+180° - 4x,解得 x=37.5°,则∠B=180° - 4x=30°;③当 DE=BE 时,则∠B=$\frac{1}{2}$(180° - 2x),由∠CDE=∠DEB+∠B,得45°+22.5°+x=2x+$\frac{1}{2}$(180° - 2x),此方程无解,
∴DE=BE 不成立.综上所述,∠B=30°.

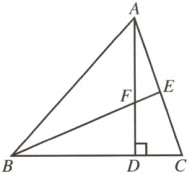
16.(8分)(林州期中)如图，在△ABC中，AD是高，BE是角平分线，它们相交于点F，∠BAC=58°，∠C=72°，求∠DAC和∠AFB的度数.

答案： 16.解:
∵AD 是高,
∴∠ADC=90°.
∵∠BAC=58°,∠C=72°,
∴∠ABC=180° - ∠BAC - ∠C=180° - 58° - 72°=50°,∠DAC=180° - ∠ADC - ∠C=180° - 90° - 72°=18°,
∴∠BAD=∠BAC - ∠DAC=58° - 18°=40°.
∵BE 是∠ABC 的平分线,
∴∠ABF=$\frac{1}{2}$∠ABC=25°,
∴∠AFB=180° - ∠ABF - ∠BAD=180° - 25° - 40°=115°.

17.(9分)如图，已知点D，E为△ABC的边BC上两点，AD=AE，BD=CE，为了判断∠B与∠C的大小关系，请你填空完成下面的推理过程，并在空白括号内注明推理的依据.

解：过点A作AH⊥BC，垂足为H.
∵在△ADE中，AD=AE(已知)，AH⊥BC(所作)，
∴DH=EH(等腰三角形底边上的高也是底边上的中线).
又BD=CE(已知)，
∴BD+DH=CE+EH(等式的性质).
即BH=CH.
又AH⊥BC，垂足为H(所作)，
∴AH为线段BC的垂直平分线.
∴AB=AC(线段垂直平分线的性质).
∴∠B=∠C(等边对等角).

答案： 17.解:过点 A 作 AH⊥BC,垂足为 H.
∵在△ADE 中,AD=AE(已知),AH⊥BC(所作),
∴DH=EH(等腰三角形底边上的高也是底边上的中线).又 BD=CE(已知),
∴BD+DH=CE+EH(等式的性质).即 BH=CH.又 AH⊥BC,垂足为 H(所作),
∴AH 为线段 BC 的垂直平分线.
∴AB=AC(线段垂直平分线的性质).∠B=∠C(等边对等角).