《2025年昕金立文化单元金卷八年级数学上册人教版》

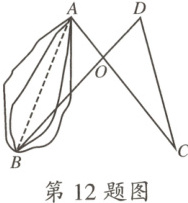
12.如图，$AC=DB$，$AO=DO$，$CD=55\ {m}$，则$A$，$B$两点之间的距离为55${m}$.

答案： 12.55

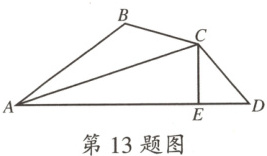
13.如图，在四边形$ABCD$中，$AC$平分$\angle BAD$，$BC=DC$，$CE\perp AD$于点$E$，$AD=12$，$AB=7$，则$DE$的长为2.5.

答案： 13.2.5

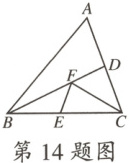
14.如图，在$\triangle ABC$中，$\triangle ABC$的面积为10，$AB=4$，$BD$平分$\angle ABC$，$E$，$F$分别为$BC$，$BD$上的动点，则$CF+EF$的最小值是5.

答案：
14.5【解析】如图,过点C作CM⊥AB于点M,交BD于点F',过点F'作F'E'⊥BC于点E'.
∵BD平分∠ABC,
∴MF'=E'F',此时CF+EF的值最小,最小值为CF+EF=CF'+MF'=CM.
∵$S_{\triangle ABC}$=$\frac{1}{2}$CM·AB=10，AB=4，
∴CM=5，即CF+EF的最小值是5.

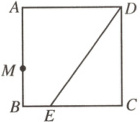
15.如图，在正方形$ABCD$中，$AB=4$，$E$是$BC$上的一点，且$CE=3$，连接$DE$，动点$M$从点$A$以每秒2个单位长度的速度沿$AB-BC-CD-DA$向终点$A$运动，设点$M$的运动时间为$t$秒，当$\triangle ABM$和$\triangle DCE$全等时，$t$的值是3.5或6.5.

答案： 15.3.5或6.5【解析】如图,分两种情况：①当点M在BC上，△ABM′≅△DCE时，BM′=CE，由题意，得BM′=2t-4=3，解得t=3.5；②当点M在AD上，△ABM″≅△CDE时，AM″=CE，由题意，得AM″=16-2t=3，解得t=6.5.所以当t的值为3.5或6.5时，△ABM和△DCE全等.

16.(8分)如图，点$E$在$\triangle ABC$外部，点$D$在$BC$边上，$DE$交$AC$于点$F$，若$\angle1=\angle2$，$\angle E=\angle C$，$AE=AC$，求证：$\triangle ABC\cong\triangle ADE$.

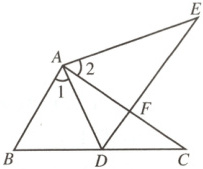
答案： 16.证明：
∵∠1=∠2，
∴∠1+∠DAC=∠2+∠DAC，
即∠BAC=∠DAE.
在△ABC和△ADE中，$\begin{cases} ∠BAC=∠DAE,\\ AC=AE,\\ ∠C=∠E,\end{cases}$
∴△ABC≅△ADE(ASA).

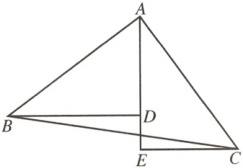
17.(9分)(信阳期中)如图，$\triangle ABD\cong\triangle CAE$，点$A$，$D$，$E$三点在一条直线上.
(1)求证：$BD=CE+DE$.
(2)当$\triangle ABD$满足什么条件时，$BD// CE$？请说明理由.

答案： 17.
(1)证明：
∵△ABD≅△CAE，
∴BD=AE，AD=CE.
又
∵AE=AD+DE，
∴BD=CE+DE.
(2)解：当△ABD满足∠ADB=90°时，BD//CE.
理由如下：
∵△ABD≅△CAE，
∴∠ADB=∠CEA.
∵∠ADB=90°，
∴∠CEA=90°，∠BDE=90°，
∴∠CEA=∠BDE，
∴BD//CE.