第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
8.已知$a=81^{7}$,$b=27^{9}$,$c=9^{13}$,则$a,b,c$的大小关系是 (
A.$a>b>c$
B.$a>c>b$
C.$a<b<c$
D.$b>c>a$
A
)A.$a>b>c$
B.$a>c>b$
C.$a<b<c$
D.$b>c>a$
答案:
8.A【解析】$\because a = 81^{7},b = 27^{9},c = 9^{13},\therefore a = (3^{4})^{7} = 3^{28},b = (3^{3})^{9} = 3^{27},c = (3^{2})^{13} = 3^{26}.\because 3^{28} > 3^{27} > 3^{26}$,$\therefore a>b>c$.故选A.
9.(鹤壁期中)如图,将四个大小相同的小正方形按如图所示的方
式放置变为一个大正方形,根据图形中阴影部分的面积,可以
验证 (
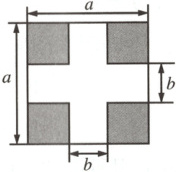
A.$(a-b)^{2}=a^{2}-2ab+b^{2}$
B.$(a+b)^{2}=a^{2}+2ab+b^{2}$
C.$(a-b)^{2}=(a+b)^{2}-4ab$
D.$(a+b)(a-b)=a^{2}-b^{2}$
式放置变为一个大正方形,根据图形中阴影部分的面积,可以
验证 (
A
)
A.$(a-b)^{2}=a^{2}-2ab+b^{2}$
B.$(a+b)^{2}=a^{2}+2ab+b^{2}$
C.$(a-b)^{2}=(a+b)^{2}-4ab$
D.$(a+b)(a-b)=a^{2}-b^{2}$
答案:
9.A
10.设$a$,$b$是实数,定义$*$的一种运算为$a*b=(a+b)^{2}$,有下列
结论:
①$a*b=0$,则$a=0$且$b=0$;
②$a*b=b*a$;
③$a*(b+c)=a*b+a*c$;
④$a*b=(-a)*(-b)$.
其中正确的有 (
A.1个
B.2个
C.3个
D.4个
结论:
①$a*b=0$,则$a=0$且$b=0$;
②$a*b=b*a$;
③$a*(b+c)=a*b+a*c$;
④$a*b=(-a)*(-b)$.
其中正确的有 (
B
)A.1个
B.2个
C.3个
D.4个
答案:
10.B【解析】$\because a * b = 0,a * b = (a + b)^{2},\therefore (a + b)^{2} = 0$,即$a + b = 0,\therefore a,b$互为相反数,故①错误;$b = (a + b)^{2},b * a = (b + a)^{2}$,故②正确;$a * (b + c) = (a + b + c)^{2},a * b + a * c = (a + b)^{2} + (a + c)^{2}$,故③错误;$a * b = (a + b)^{2},(-a) * (-b) = (-a - b)^{2}$,$\because (a + b)^{2} = (-a - b)^{2},\therefore a * b = (-a) * (-b)$,故④正确.综上所述,正确的有2个.故选B.
11.已知单项式$3x^{2}y^{3}$与$2xy^{2}$的积为$mx^{3}y^{n}$,则$m-n=$
1
.
答案:
11.1
12.若$(x+2)(x+3)=7$,则$2-10x-2x^{2}$的值为
0
.
答案:
12.0
13.小明将$(2024x+2025)^{2}$展开后得到$a_{1}x^{2}+b_{1}x+c_{1}$,小李将
$(2025x+2024)^{2}$展开后得到$a_{2}x^{2}+b_{2}x+c_{2}$,若两人计算过程无
误,则$a_{1}-a_{2}$的值为_______.
$(2025x+2024)^{2}$展开后得到$a_{2}x^{2}+b_{2}x+c_{2}$,若两人计算过程无
误,则$a_{1}-a_{2}$的值为_______.
答案:
$-4049$。
14.如图,大正方形与小正方形的面积之差是36,则阴影部分的面
积是
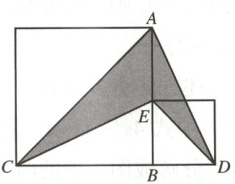
积是
18
.
答案:
14.18 【解析】$\because$大正方形的面积为$AB^{2}$,小正方形的面积为$BE^{2}$,$\therefore AB^{2} - BE^{2} = 36.\because BC = AB,BD = BE$,$\therefore S_{阴影}=S_{\triangle ACE}+S_{\triangle AED}=\frac{1}{2}AE· BC+\frac{1}{2}AE· BD=\frac{1}{2}AE(BC + BD)=\frac{1}{2}(AB - BE)(AB + BE)=\frac{1}{2}(AB^{2}-BE^{2})=\frac{1}{2}×36 = 18$.
15.南宋数学家杨辉在其著作《详解九章算法》中揭示了$(a+b)^{n}$($n$
为非负整数)展开式的项数及各项系数的有关规律如下,后人也
将下表称为“杨辉三角”,则$(a+b)^{2025}$展开式中所有项的系数
和是

$(a+b)^{0}=1$
$(a+b)^{1}=a+b$
$(a+b)^{2}=a^{2}+2ab+b^{2}$
$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$
$(a+b)^{4}=a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4}$
$(a+b)^{5}=a^{5}+5a^{4}b+10a^{3}b^{2}+10a^{2}b^{3}+5ab^{4}+b^{5}$
$\ldots\ldots$
为非负整数)展开式的项数及各项系数的有关规律如下,后人也
将下表称为“杨辉三角”,则$(a+b)^{2025}$展开式中所有项的系数
和是
$2^{2025}$
.
$(a+b)^{0}=1$
$(a+b)^{1}=a+b$
$(a+b)^{2}=a^{2}+2ab+b^{2}$
$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$
$(a+b)^{4}=a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4}$
$(a+b)^{5}=a^{5}+5a^{4}b+10a^{3}b^{2}+10a^{2}b^{3}+5ab^{4}+b^{5}$
$\ldots\ldots$
答案:
15.$2^{2025}$
查看更多完整答案,请扫码查看


