第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
22.(10 分)在 Rt△ABC 中,$∠ACB = 90^{\circ}$,$∠A = 30^{\circ}$,BD 是△ABC 的角平分线,$DE ⊥ AB$于点 E.
(1)如图 1,连接 EC,求证:△EBC 是等边三角形;
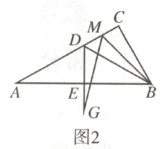
(2)如图 2,点 M 是线段 CD 上的一点(不与点 C,D 重合),以 BM 为一边,在 BM 的下方作$∠BMG = 60^{\circ}$,MG 交 DE 延长线于点 G,求出 MD,DG 与 AD 之间的数量关系.
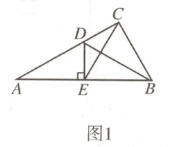
(1)如图 1,连接 EC,求证:△EBC 是等边三角形;
(2)如图 2,点 M 是线段 CD 上的一点(不与点 C,D 重合),以 BM 为一边,在 BM 的下方作$∠BMG = 60^{\circ}$,MG 交 DE 延长线于点 G,求出 MD,DG 与 AD 之间的数量关系.


答案:
(1)证明:在$Rt\triangle ABC$中,$\angle ACB=90°$,$\angle A=30°$,$\therefore \angle ABC=60°$,$BC=\frac{1}{2}AB.$
$\because BD$平分$\angle ABC$,$\therefore \angle DBC=\angle DBA=\angle A=30°$,$\therefore DA=DB.$
$\because DE\perp AB$于点$E$,$\therefore AE=BE=\frac{1}{2}AB$,$\therefore BC=BE$,$\therefore \triangle EBC$是等边三角形.
(2)解:如图,延长$ED$至点$W$,使得$DW = MD$,连接$MW.$
由
(1)可知$DA = DB.$
$\because DE\perp AB$,$\angle A=30°$,$\therefore \angle ADE=\angle BDE=60°.$
$\because MD = DW$,$\angle WDM=\angle ADE=60°$,$\therefore \triangle WDM$是等边三角形,$\therefore MW = MD$,$\angle WMD=60°.$
又$\angle BMG=60°$,$\therefore \angle WMG=\angle DMB.$
又$\angle W=\angle MDB$,$\therefore \triangle WGM\cong\triangle DBM$,$\therefore DB = WG=DG + MD$,$\therefore AD=DG + MD.$

(1)证明:在$Rt\triangle ABC$中,$\angle ACB=90°$,$\angle A=30°$,$\therefore \angle ABC=60°$,$BC=\frac{1}{2}AB.$
$\because BD$平分$\angle ABC$,$\therefore \angle DBC=\angle DBA=\angle A=30°$,$\therefore DA=DB.$
$\because DE\perp AB$于点$E$,$\therefore AE=BE=\frac{1}{2}AB$,$\therefore BC=BE$,$\therefore \triangle EBC$是等边三角形.
(2)解:如图,延长$ED$至点$W$,使得$DW = MD$,连接$MW.$
由
(1)可知$DA = DB.$
$\because DE\perp AB$,$\angle A=30°$,$\therefore \angle ADE=\angle BDE=60°.$
$\because MD = DW$,$\angle WDM=\angle ADE=60°$,$\therefore \triangle WDM$是等边三角形,$\therefore MW = MD$,$\angle WMD=60°.$
又$\angle BMG=60°$,$\therefore \angle WMG=\angle DMB.$
又$\angle W=\angle MDB$,$\therefore \triangle WGM\cong\triangle DBM$,$\therefore DB = WG=DG + MD$,$\therefore AD=DG + MD.$

23.(11 分)先阅读下面的内容,再解答问题.
【阅读】例:求多项式$m^2 + 2mn + 2n^2 - 6n + 13$的最小值.
解:$m^2 + 2mn + 2n^2 - 6n + 13 = (m^2 + 2mn + n^2) + (n^2 - 6n + 9) + 4 = (m + n)^2 + (n - 3)^2 + 4$.
$\because (m + n)^2 \geq 0$,$(n - 3)^2 \geq 0$,
$\therefore (m + n)^2 + (n - 3)^2 + 4 \geq 4$,
$\therefore$多项式$m^2 + 2mn + 2n^2 - 6n + 13$的最小值是 4.
【解答问题】
(1)请用 x,y 表示出例题在解答过程中因式分解运用的公式
(2)已知 a,b,c 是△ABC 的三边,且满足$a^2 + b^2 = 10a + 8b - 41$,求第三边 c 的取值范围;
(3)求多项式$-2x^2 + 4xy - 3y^2 - 6y + 7$的最大值.
【阅读】例:求多项式$m^2 + 2mn + 2n^2 - 6n + 13$的最小值.
解:$m^2 + 2mn + 2n^2 - 6n + 13 = (m^2 + 2mn + n^2) + (n^2 - 6n + 9) + 4 = (m + n)^2 + (n - 3)^2 + 4$.
$\because (m + n)^2 \geq 0$,$(n - 3)^2 \geq 0$,
$\therefore (m + n)^2 + (n - 3)^2 + 4 \geq 4$,
$\therefore$多项式$m^2 + 2mn + 2n^2 - 6n + 13$的最小值是 4.
【解答问题】
(1)请用 x,y 表示出例题在解答过程中因式分解运用的公式
$x^{2}+2xy + y^{2}=(x + y)^{2}$
;(2)已知 a,b,c 是△ABC 的三边,且满足$a^2 + b^2 = 10a + 8b - 41$,求第三边 c 的取值范围;
(3)求多项式$-2x^2 + 4xy - 3y^2 - 6y + 7$的最大值.
答案:
解:
(1)$x^{2}+2xy + y^{2}=(x + y)^{2}$
(2)$\because a^{2}+b^{2}=10a + 8b-41$,$\therefore a^{2}-10a + 25 + b^{2}-8b + 16 = 0$,$\therefore (a - 5)^{2}+(b - 4)^{2}=0.$
$\because (a - 5)^{2}\geq0$,$(b - 4)^{2}\geq0$,$\therefore a - 5 = 0$,$b - 4 = 0$,$\therefore a = 5$,$b = 4$,$\therefore 5 - 4<c<5 + 4$,即$1<c<9$.
(3)原式$=-2x^{2}+4xy-2y^{2}-y^{2}-6y-9 + 16=-2(x - y)^{2}-(y + 3)^{2}+16.$
$\because -2(x - y)^{2}\leq0$,$-(y + 3)^{2}\leq0$,$\therefore$多项式$-2x^{2}+4xy-3y^{2}-6y + 7$的最大值是$16.$
(1)$x^{2}+2xy + y^{2}=(x + y)^{2}$
(2)$\because a^{2}+b^{2}=10a + 8b-41$,$\therefore a^{2}-10a + 25 + b^{2}-8b + 16 = 0$,$\therefore (a - 5)^{2}+(b - 4)^{2}=0.$
$\because (a - 5)^{2}\geq0$,$(b - 4)^{2}\geq0$,$\therefore a - 5 = 0$,$b - 4 = 0$,$\therefore a = 5$,$b = 4$,$\therefore 5 - 4<c<5 + 4$,即$1<c<9$.
(3)原式$=-2x^{2}+4xy-2y^{2}-y^{2}-6y-9 + 16=-2(x - y)^{2}-(y + 3)^{2}+16.$
$\because -2(x - y)^{2}\leq0$,$-(y + 3)^{2}\leq0$,$\therefore$多项式$-2x^{2}+4xy-3y^{2}-6y + 7$的最大值是$16.$
查看更多完整答案,请扫码查看


