第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
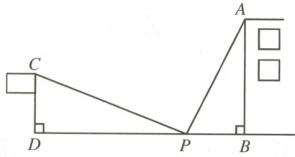
17.(9分)(信阳月考)如图,阳阳为了测量楼AB的高,在旗杆CD与楼之间选定一点P,量得点P到楼底的距离PB与旗杆的高度CD相等,均为10米,量得旗杆与楼之间距离DB = 36米.若∠CPD = 36°,∠APB = 54°,求楼AB的高.

答案:
17.解:
∵∠CPD = 36°,∠APB = 54°,∠CDP = ∠PBA = 90°,
∴∠PCD = ∠APB = 54°。
又∠CDP = ∠PBA,CD = PB,
∴△CPD ≌ △PAB,
∴DP = AB。
∵DB = 36米,PB = 10米,
∴AB = DP = DB - PB = 36 - 10 = 26(米)。
答:楼AB的高是26米。
∵∠CPD = 36°,∠APB = 54°,∠CDP = ∠PBA = 90°,
∴∠PCD = ∠APB = 54°。
又∠CDP = ∠PBA,CD = PB,
∴△CPD ≌ △PAB,
∴DP = AB。
∵DB = 36米,PB = 10米,
∴AB = DP = DB - PB = 36 - 10 = 26(米)。
答:楼AB的高是26米。
18.(9分)下面是多媒体上展示的一道习题,请你将解题过程补充完整.
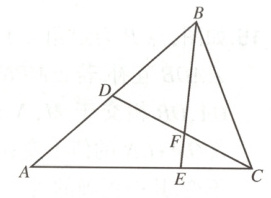
如图,在△ABC中,∠ABC = ∠ACB,点D,E分别在边AB,AC上,∠A = ∠ABE,∠CDB = ∠CBD,BE与CD交于点F,判断∠BDF与∠BFD的数量关系,并说明理由.
解:∠BDF与∠BFD的数量关系是
理由:设∠A = α,∠ABC = β,
∵∠ABC = ∠ACB,
∴α + 2β =
又∠A = ∠ABE = α,
∴∠CBF = ∠ABC - ∠
∵∠CDB = ∠CBD = β,
∴∠DCB = 180° - ∠CBD - ∠CDB =
∵∠BFD是△BCF的外角,
∴∠BFD = ∠
∴∠BDF与∠BFD的数量关系是
如图,在△ABC中,∠ABC = ∠ACB,点D,E分别在边AB,AC上,∠A = ∠ABE,∠CDB = ∠CBD,BE与CD交于点F,判断∠BDF与∠BFD的数量关系,并说明理由.
解:∠BDF与∠BFD的数量关系是
∠BDF = ∠BFD
.
理由:设∠A = α,∠ABC = β,
∵∠ABC = ∠ACB,
∴α + 2β =
180
°.又∠A = ∠ABE = α,
∴∠CBF = ∠ABC - ∠
ABE
=β - α
.∵∠CDB = ∠CBD = β,
∴∠DCB = 180° - ∠CBD - ∠CDB =
180° - 2β
.∵∠BFD是△BCF的外角,
∴∠BFD = ∠
CBF
+ ∠DCB
=180° - β - α
.∴∠BDF与∠BFD的数量关系是
∠BDF = ∠BFD
.
答案:
18.解:∠BDF与∠BFD的数量关系是∠BDF = ∠BFD,理由如下:
设∠A = α,∠ABC = β。
∵∠ABC = ∠ACB,
∴α + 2β = 180°。
又∠A = ∠ABE = α,
∴∠CBF = ∠ABC - ∠ABE = β - α。
∵∠CDB = ∠CBD = β,
∴∠DCB = 180° - ∠CBD - ∠CDB = 180° - 2β。
∵∠BFD是△BCF的外角,
∴∠BFD = ∠CBF + ∠DCB = β - α + 180° - 2β = 180° - β - α。
又∠BDF = 180° - β - α,
∴∠BDF与∠BFD的数量关系是∠BDF = ∠BFD。
设∠A = α,∠ABC = β。
∵∠ABC = ∠ACB,
∴α + 2β = 180°。
又∠A = ∠ABE = α,
∴∠CBF = ∠ABC - ∠ABE = β - α。
∵∠CDB = ∠CBD = β,
∴∠DCB = 180° - ∠CBD - ∠CDB = 180° - 2β。
∵∠BFD是△BCF的外角,
∴∠BFD = ∠CBF + ∠DCB = β - α + 180° - 2β = 180° - β - α。
又∠BDF = 180° - β - α,
∴∠BDF与∠BFD的数量关系是∠BDF = ∠BFD。
19.(9分)在△ABC中,AD是∠BAC的角平分线,∠B<∠C,
(1)如图1,AE是△ABC边BC上的高,∠B = 36°,∠C = 70°,求∠DAE的度数;
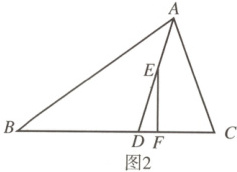
(2)如图2,点E在AD上,EF⊥BC于点F,猜想∠DEF与∠B,∠C的数量关系,并证明你的结论.
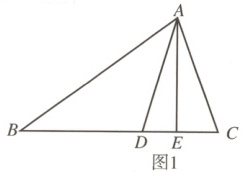
(1)如图1,AE是△ABC边BC上的高,∠B = 36°,∠C = 70°,求∠DAE的度数;
(2)如图2,点E在AD上,EF⊥BC于点F,猜想∠DEF与∠B,∠C的数量关系,并证明你的结论.


答案:
19.解:
(1)
∵AD平分∠BAC,
∴∠CAD = $\frac{1}{2}$∠BAC。
∵AE⊥BC,
∴∠CAE = 90° - ∠C,
∴∠DAE = ∠CAD - ∠CAE = $\frac{1}{2}$∠BAC - (90° - ∠C) = $\frac{1}{2}$(180° - ∠B - ∠C) - (90° - ∠C) = $\frac{1}{2}$∠C - $\frac{1}{2}$∠B = $\frac{1}{2}$(∠C - ∠B)。
∵∠B = 36°,∠C = 70°,
∴∠DAE = $\frac{1}{2}$(70° - 36°) = 17°。
(2)结论:∠DEF = $\frac{1}{2}$(∠C - ∠B)。
证明:如图,过点A作AG⊥BC于点G。
又EF⊥BC,
∴AG//EF,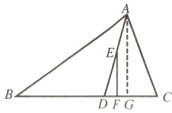
∴由
(1)可得∠DAG = ∠DEF,∠DAG = $\frac{1}{2}$(∠C - ∠B)。
∴∠DEF = $\frac{1}{2}$(∠C - ∠B)。
19.解:
(1)
∵AD平分∠BAC,
∴∠CAD = $\frac{1}{2}$∠BAC。
∵AE⊥BC,
∴∠CAE = 90° - ∠C,
∴∠DAE = ∠CAD - ∠CAE = $\frac{1}{2}$∠BAC - (90° - ∠C) = $\frac{1}{2}$(180° - ∠B - ∠C) - (90° - ∠C) = $\frac{1}{2}$∠C - $\frac{1}{2}$∠B = $\frac{1}{2}$(∠C - ∠B)。
∵∠B = 36°,∠C = 70°,
∴∠DAE = $\frac{1}{2}$(70° - 36°) = 17°。
(2)结论:∠DEF = $\frac{1}{2}$(∠C - ∠B)。
证明:如图,过点A作AG⊥BC于点G。
又EF⊥BC,
∴AG//EF,

∴由
(1)可得∠DAG = ∠DEF,∠DAG = $\frac{1}{2}$(∠C - ∠B)。
∴∠DEF = $\frac{1}{2}$(∠C - ∠B)。
查看更多完整答案,请扫码查看


