《2025年昕金立文化单元金卷八年级数学上册人教版》

4.已知点M(a,b)与点N(2,5)关于x轴对称，则a - b的值为
(A)

A.7
B.-7
C.3
D.-3

答案： A

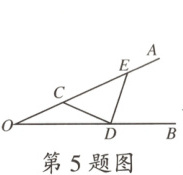
5.“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助“三等分角仪”能三等分任一角.如图，这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在点O相连并可绕O转动，点C固定，OC = CD = DE，点D，E可在槽中滑动，若∠BDE = 75°，则∠O的度数是
(C)

A.15°
B.20°
C.25°
D.30°

答案： C

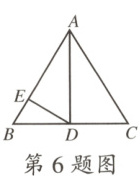
6.(长葛期中)如图，在等边三角形ABC中，AD平分∠BAC，DE⊥AB于点E，若AC = 8，则BE =
(B)

A.1
B.2
C.3
D.4

答案： B

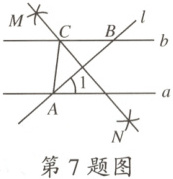
7.如图，已知a//b，直线l与直线a，b分别交于点A，B，分别以点A，B为圆心，大于$\frac{1}{2}AB$的长为半径画弧，两弧相交于点M，N，作直线MN，交直线b于点C，连接AC，若∠1 = 38°，则∠ACB的度数是
(C)

A.98°
B.102°
C.104°
D.108°

答案： C

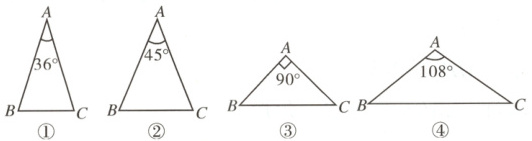
8.如图，下列四个三角形中，均有AB = AC，则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是
( )



A.①③
B.①②④
C.①③④
D.①②③④

答案： C

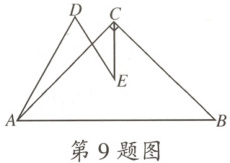
9.(商丘期末)如图，在Rt△ABC中，∠ACB = 90°，CA = CB，∠BAD = ∠ADE = 60°，DE = 3，AB = 10，CE平分∠ACB，DE与CE相交于点E，则AD的长为
(D)

A.4
B.13
C.6.5
D.7

答案：
9.D [解析]如图,延长DE交AB于点F,延长CE交AB于点G.
∵∠BAD = ∠D = 60°,
∴△ADF是等边三角形，
∴AD = AF = DF,∠AFD = 60°.
∵CA = CB,CE平分∠ACB,
∴CG⊥AB,即∠CGB = 90°,AG = $\frac{1}{2}$AB = 5.设AD = AF = DF = a,则EF = DF - DE = a - 3.在Rt△GEF中,∠AFD = 60°,
∴∠FEG = 30°,
∴GF = $\frac{1}{2}$EF = $\frac{1}{2}$(a - 3).由AF - GF = AG,得a - $\frac{1}{2}$(a - 3) = 5,解得a = 7.故选D.