《2026年零差错高中数学必修第一册人教版》

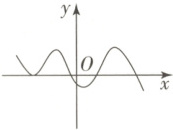
1. 已知函数 $ y = f(x) $ 的图象如图所示，其中零点的个数与可以用二分法求其零点近似值的个数分别是（C）

A.$ 4,4 $
B.$ 3,4 $
C.$ 4,3 $
D.$ 5,4 $

答案： 1.C[详解]函数图象与x轴有4个交点，所以零点的个数为4.左、右函数值异号的零点有3个，所以可以用二分法求解的个数为3.

2. 用二分法研究函数 $ f(x) = x^{5} + 8x^{3} - 1 $ 的零点时，第一次经过计算得 $ f(0) ＜ 0 $，$ f(0.5) ＞ 0 $，则其中一个零点所在区间和第二次应计算的函数值分别为（B）

A.$ (0,0.5) $，$ f(0.125) $
B.$ (0,0.5) $，$ f(0.25) $
C.$ (0.5,1) $，$ f(0.75) $
D.$ (0,0.5) $，$ f(0.375) $

答案： 2.B[详解]因为f
(0)f(0.5)＜0，由零点存在定理知零点x₀∈(0,0.5)，根据二分法知，第二次应计算f($\frac{0 + 0.5}{2}$)，即f(0.25).

3. 已知函数 $ y = f(x) $ 为 $ [0,1] $ 上的连续函数，且 $ f(0) · f(1) ＜ 0 $，使用二分法求函数零点，要求近似值的精确度达到 $ 0.1 $，则需对区间至少分（C）

A.$ 2 $ 次
B.$ 3 $ 次
C.$ 4 $ 次
D.$ 5 $ 次

答案： 3.C[详解]每经过一次操作，零点所在范围变成原来的一半，经过n次后，所给的范围变成$\frac{1}{2^n}$，则$\frac{1}{2^n}$≤0.1，即n≥4，又n∈N*，故对区间只需要分4次即可.

1. 【题型一】下列函数图象与 $ x $ 轴均有交点，但不宜用二分法求交点横坐标的是（B）

答案： 1.B[详解]二分法求零点，要求函数连续不断且满足零点存在定理，即f(a)f(b)＜0成立，对比选项可知A,C,D均符合，对于B，f(a)f(b)≥0恒成立，不满足零点存在定理，故B错误.

2. 【题型一】（2025·广东深圳外国语高级中学期末）用二分法求方程 $ \sqrt{x} - 3^{-x} = 0 $ 的近似解时，所取的第一个区间可以是（B）

A.$ (0,\frac{1}{3}) $
B.$ (\frac{1}{3},\frac{1}{2}) $
C.$ (\frac{1}{2},\frac{2}{3}) $
D.$ (\frac{2}{3},1) $

答案： 2.B[详解]令f(x)=$\sqrt{x}$ - 3⁻ˣ，则f
(0)=0 - 1 = -1＜0，f($\frac{1}{3}$)=$\sqrt{\frac{1}{3}}$ - 3⁻¹/³=$\frac{1}{\sqrt{3}}$ - $\frac{1}{\sqrt[3]{3}}$＜0，f($\frac{1}{2}$)=$\sqrt{\frac{1}{2}}$ - 3⁻¹/²=$\frac{1}{\sqrt{2}}$ - $\frac{1}{\sqrt{3}}$＞0，f
(1)=$\sqrt{1}$ - 3⁻¹=1 - $\frac{1}{3}$＞0，得f($\frac{1}{3}$)·f($\frac{1}{2}$)＜0，可知所取区间为($\frac{1}{3}$,$\frac{1}{2}$).

3. 【题型二】某同学用二分法求函数 $ f(x) = e^{x} + x - 5 $ 的零点时，用计算器算得部分函数值如下表。

则该函数零点的近似值（精确度为 $ 0.1 $）可以是（C）

A.$ 1.2 $
B.$ 1.21 $
C.$ 1.27 $
D.$ 1.32 $

答案： 3.C[详解]f(1.25)≈ - 0.260＜0，f(1.3125)≈0.028＞0，由零点存在定理，得区间(1.25,1.3125)内存在零点，由于1.27∈(1.25,1.3125)，1.2,1.21,1.32∉(1.25,1.3125)，故该函数零点的近似值(精确度为0.1)可以是1.27.

4. 【题型三】函数 $ f(x) = 2^{x} + \log_{2}(x - 1) - \frac{a}{2} $ 的零点在区间 $ (2,3) $ 内，则实数 $ a $ 的取值范围为（D）

A.$ (4,\frac{9}{2}) $
B.$ (4,18) $
C.$ (8,9) $
D.$ (8,18) $

答案： 4.D[详解]函数f(x)=2ˣ + log₂(x - 1) - $\frac{a}{2}$在定义域(1,+∞)上连续且单调递增，又函数零点在区间(2,3)内，则f
(2)＜0，f
(3)＞0，得关于a的不等式，解得a∈(8,18).