《2026年零差错高中数学必修第一册人教版》

1. (2025·辽宁东北育才学校月考)已知集合$A=\{(x,y)|x,y\in\mathbf{N}^*,y\geqslant x\}$，$B=\{(x,y)|x+y=8\}$，则$A\cap B$中元素的个数为（C）

A.$2$
B.$3$
C.$4$
D.$6$

答案： 1.C【详解】由题意,A∩B中的元素满足$\begin{cases}y\geq x,\\x+y=8,\end{cases}$且$x,y\in\mathbf{N}^*$,由$x+y=8\geq2x$,得$x\leq4$,所以满足$x+y=8$的有$(1,7)$,$(2,6)$,$(3,5)$,$(4,4)$,故$A\cap B$中元素的个数为4.

2. (2025·辽宁沈阳市郊联合期中)命题$p$：$\forall x\notin\{x|1\leqslant x\leqslant5\}$，$x^2 - 4x＞5$，则命题$p$的否定是（B）

A.$\exists x\in\{x|1\leqslant x\leqslant5\}$，$x^2 - 4x\leqslant5$
B.$\exists x\notin\{x|1\leqslant x\leqslant5\}$，$x^2 - 4x\leqslant5$
C.$\forall x\notin\{x|1\leqslant x\leqslant5\}$，$x^2 - 4x\leqslant5$
D.$\forall x\in\{x|1\leqslant x\leqslant5\}$，$x^2 - 4x\leqslant5$

答案： 2.B【详解】$p:\forall x\notin\{x|1\leq x\leq5\},x^2-4x＞5$,否定是$\exists x\notin\{x|1\leq x\leq5\},x^2-4x\leq5$.

3. (2025·吉林“BEST 合作体”高一上期末)已知集合$A=\{-4,-2,0,2\}$，$B=\left\{x\left|\dfrac{x}{x + 1}\in\mathbf{Z},x\in A\right.\right\}$，则$A\cap B$等于（B）

A.$\{0\}$
B.$\{-2,0\}$
C.$\{0,2\}$
D.$\{-2,0,2\}$

答案： 3.B【详解】当$x=-4$时,$\frac{x}{x+1}-\frac{4}{3}\notin\mathbf{Z}$;当$x=-2$时,$\frac{x}{x+1}=2\in\mathbf{Z}$;当$x=0$时,$\frac{x}{x+1}=0\in\mathbf{Z}$;当$x=2$时,$\frac{x}{x+1}=\frac{2}{3}\notin\mathbf{Z}$,$\therefore B=\{-2,0\}$,$\therefore A\cap B=\{-2,0\}$.

4. (2025·辽宁大连第八中学月考)$A=\{1,x,y\}$，$B=\{1,x^2,2y\}$，若$A = B$，则实数$x$的取值集合为（A）

A.$\left\{\dfrac{1}{2}\right\}$
B.$\left\{\dfrac{1}{2},-\dfrac{1}{2}\right\}$
C.$\left\{0,-\dfrac{1}{2}\right\}$
D.$\left\{0,\dfrac{1}{2},-\dfrac{1}{2}\right\}$

答案： 4.A【详解】由题意$x\neq1$,$\begin{cases}x=2y,\\y=x^2,\end{cases}$或$\begin{cases}x=x^2,\\y=2y,\end{cases}$解得$\begin{cases}x=-\frac{1}{2},\\y=\frac{1}{4}\end{cases}$或$\begin{cases}x=0,\\y=0,\end{cases}$由集合中元素互异性可知集合为$\{\frac{1}{2}\}$

5. (2025·辽宁朝阳市重点高中高一上联考)命题“$\exists x\in\mathbf{R}$，$\dfrac{1}{2}x^2 + x - \dfrac{3}{2} - a＜0$”为真命题的一个必要不充分条件是（D）

A.$a\geqslant0$
B.$a\geqslant1$
C.$a＞-2$
D.$a\geqslant - 3$

答案： 5.D【详解】由$\exists x\in\mathbf{R},\frac{1}{2}x^2+x-\frac{3}{2}-a＜0$,可得$a＞\frac{1}{2}x^2+x-\frac{3}{2}$在$\mathbf{R}$上能成立,因$\frac{1}{2}x^2+x-\frac{3}{2}=\frac{1}{2}(x+1)^2-2\geq-2$,故得$a＞-2$.故$a＞-2$的一个必要不充分条件是$a\geq-3$.

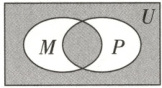
6. (2025·吉林东北师大附中高一上检测)已知全集$U=\{1,2,3,4,5,6,7,8\}$，$M=\{1,3,6\}$，$P=\{3,4,5\}$，指出 Venn 图中阴影部分表示的集合是（C）


A.$\{3\}$
B.$\{1,4,5,6\}$
C.$\{2,3,7,8\}$
D.$\{2,7,8\}$

答案： 6.C【详解】因为$M=\{1,3,6\}$,$P=\{3,4,5\}$,所以$M\cap P=\{3\}$,$M\cup P=\{1,3,4,5,6\}$.因为$U=\{1,2,3,4,5,6,7,8\}$,所以$\complement_U(M\cup P)=\{2,7,8\}$.由Venn图易知,图中阴影部分表示的集合是$(M\cap P)\cup\complement_U(M\cup P)$,故Venn图中阴影部分表示的集合是$\{2,3,7,8\}$.

7. (2025·辽宁东北育才学校月考)设集合$A$，$B$，$C$均为非空集合，下列命题为真命题的是（C）

A.若$A\cap B = B\cap C$，则$A = C$
B.若$A\cup B = B\cup C$，则$A = C$
C.若$A\cap B = B\cup C$，则$C\subseteq B$
D.若$A\cup B = B\cap C$，则$C\subseteq B$

答案： 7.C【详解】对于A,$A\cap B=B\cap C$,当$A=\{1,2\}$,$B=\{1\}$,$C=\{1,2,3\}$时,结论不成立,则A错误;对于B,$A\cup B=B\cup C$,当$A=\{1,2\}$,$B=\{3\}$,$C=\{1,2,3\}$时,结论不成立,则B错误;对于C,因为$(A\cap B)\subseteq B$,$A\cap B=B\cap C$,所以$(B\cap C)\subseteq B$.又$B\subseteq(B\cup C)$,所以$B=B\cup C$,则$C\subseteq B$,则C正确;对于D,$A\cup B=B\cap C$,当$A=\{1\}$,$B=\{1,2\}$,$C=\{1,2,3\}$时,结论不成立,则D错误.

8. (2025·黑龙江五校期末联考)已知有$A$，$B$，$C$，$D$四个命题，其中$A$为$B$的必要条件，$B$为$C$的充分条件，$C$为$D$的必要条件，$D$为$A$的必要条件。若增加条件使得$A$，$B$，$C$，$D$中的任意一个命题均为$A$，$B$，$C$，$D$四个命题的必要条件，则这个条件可以为（A）

A.$B$为$C$的必要条件
B.$B$为$A$的必要条件
C.$C$为$D$的充分条件
D.$B$为$D$的必要条件

答案： 8.A【详解】因为A为B的必要条件,B为C的充分条件,C为D的必要条件,D为A的必要条件,即$A\Leftarrow B,B\Rightarrow C,C\Leftarrow D,D\Rightarrow A$,即$A\Leftarrow B\Leftrightarrow C\Leftarrow D\Leftarrow A$,对于A,若B为C的必要条件,即$B\Leftarrow C$,则$A\Leftarrow B\Leftrightarrow C\Leftarrow D\Leftarrow A$,所以A,B,C,D互为充要条件,则A,B,C,D中的任意一个命题均为A,B,C,D四个命题的必要条件,故A正确;对于B,若B为A的必要条件,即$B\Leftarrow A$,则$A\Leftrightarrow B\Leftrightarrow C\Leftrightarrow D\Leftarrow A$,易得B不是C的必要条件,故B错误;对于C,若C为D的充分条件,即$C\Rightarrow D$,则$A\Leftrightarrow B\Leftrightarrow C\Leftrightarrow D$,易得B不是C的必要条件,故C错误;对于D,若B为D的必要条件,即$B\Leftarrow D$,则$A\Leftrightarrow B\Leftrightarrow C\Leftrightarrow D\Leftarrow A$且$B\Leftarrow D$,易得B不是C的必要条件,故D错误.

9. (2025·吉林长春市三校联考)已知命题“$\exists x\in\{x|-2＜x＜3\}$，使得等式$3x - m = 0$成立”是假命题，则实数$m$的取值范围是$m\leq-6$或$m\geq9$。

答案： 9.$m\leq-6$或$m\geq9$【详解】由题意得“$\forall x\in\{x|-2＜x＜3\}$,使得等式$3x-m\neq0$成立”是真命题,故$m\notin(-6,9)$,所以实数$m$的取值范围是$m\leq-6$或$m\geq9$.

10. (2025·安徽马鞍山月考)已知$p$：关于$x$的方程$x^2 - 2ax + a^2 + a - 1 = 0$有实数根，$q$：$m - 1\leqslant a\leqslant m + 2$。
(1)若命题$\neg p$是真命题，求实数$a$的取值范围；
(2)若$p$是$q$的必要不充分条件，求实数$m$的取值范围。

答案： 10.解:
(1)因为命题$\neg p$是真命题,所以命题p是假命题,即关于x的方程$x^2-2ax+a^2+a-1=0$无实数根,因此,$\Delta=4a^2-4(a^2+a-1)＜0$,解得$a＞1$,所以实数的取值范围是$a＞1$.