2026年零差错高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年零差错高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
7. 【题型一】(2025·陕西西安期末)我国著名数学家华罗庚先生曾说,数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休。在数学的学习和研究中,经常用函数的图象研究函数的性质,也常利用函数的解析式来琢磨函数图象的特征。函数$f(x)=\frac{x}{x^2 - 1}$的图象大致是(
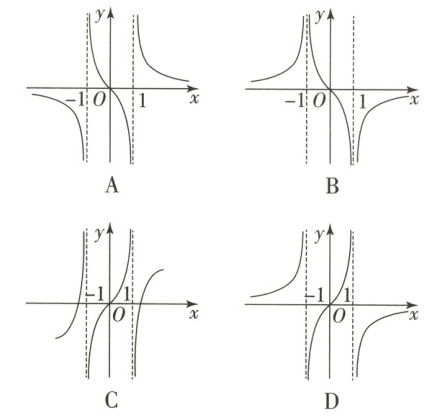
A
)
答案:
7.A【详解】$f(2) = \frac{2}{2^2 - 1} = \frac{2}{3} > 0$,$f(\frac{1}{2}) = \frac{\frac{1}{2}}{(\frac{1}{2})^2 - 1} = -\frac{2}{3} < 0$,所以C错误。
8. 【题型一】(2025·浙江衢州期末)函数$f(x)=(x + 1)^2(x - 2)$的部分图象大致为(
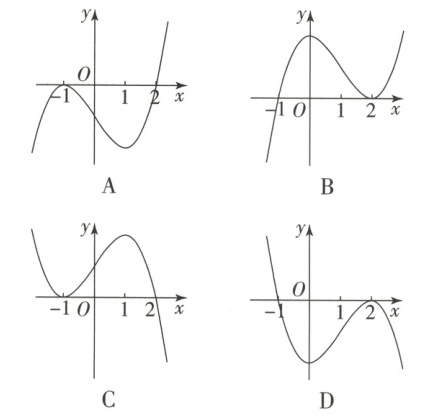
A
)
答案:
8.A【详解】由题意知$x > 2$时,$f(x) > 0$,排除C,D;$f(0) = -2 < 0$,可以排除B。
9. 【题型二】如图,四边形$BCDE$是矩形,$BC = 8$,$CD = 6$,$\triangle ABE$是等腰直角三角形。点$M$从点$A$出发,沿着边$AB$,$BC$运动到点$C$,点$N$在边$AE$,$ED$上运动,直线$MN // CD$。设点$M$运动的路程为$x$,$MN$的左侧部分的多边形的周长(含线段$MN$的长度)为$L(x)$。当点$M$在线段$BC$上运动时,$L(x)$的解析式为(
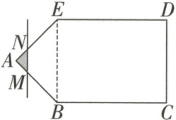
A.$L(x)=2x + 6(3\sqrt{2}\leq x\leq3\sqrt{2}+8)$
B.$L(x)=2x + 6(0\leq x\leq8)$
C.$L(x)=2x + 6\sqrt{2}+6(3\sqrt{2}\leq x\leq3\sqrt{2}+8)$
D.$L(x)=2x + 6\sqrt{2}(0\leq x\leq8)$
A
)
A.$L(x)=2x + 6(3\sqrt{2}\leq x\leq3\sqrt{2}+8)$
B.$L(x)=2x + 6(0\leq x\leq8)$
C.$L(x)=2x + 6\sqrt{2}+6(3\sqrt{2}\leq x\leq3\sqrt{2}+8)$
D.$L(x)=2x + 6\sqrt{2}(0\leq x\leq8)$
答案:
9.A【详解】因为$\triangle ABE$是等腰直角三角形,$BE = CD = 6$,所以$AB = 3\sqrt{2}$,当点$M$在线段$BC$上运动时,$3\sqrt{2} \leq x \leq 3\sqrt{2} + 8$,$L(x) = 2x + 6$。
10. 【题型一】(2025·江苏苏州期末)函数$y = f(x)$的图象如图①所示,则如图②所示的图象对应的函数解析式可能为(
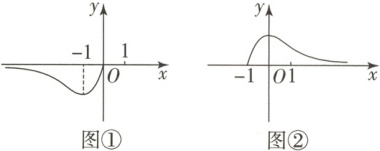
A.$y = f(-x)+1$
B.$y = f(-x + 1)$
C.$y = -f(x + 1)$
D.$y = -f(-x - 1)$
D
)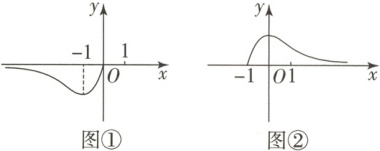
A.$y = f(-x)+1$
B.$y = f(-x + 1)$
C.$y = -f(x + 1)$
D.$y = -f(-x - 1)$
答案:
10.D【详解】先将函数$y = f(x)$的图象关于原点对称,可得到函数$y = -f(-x)$的图象,如图所示。再把所得函数图象向左平移1个单位长度,即可得到题图②所示图象,故题图②所示的图象对应的函数解析式为$y = -f(-(x + 1)) = -f(-x - 1)$。
11. 【题型一、三】已知函数$f(x)=\begin{cases}0,x < 1,\\x + 1,1\leq x < 2,\\-x^2 + 5,x\geq2,\end{cases}$若$f[f(a)] = 1$,则$a$的值为(
A.$4$
B.$3$
C.$2$
D.$1$
D
)A.$4$
B.$3$
C.$2$
D.$1$
答案:
11.D【详解】因为$f(x) = \begin{cases}0, x < 1,\\x + 1, 1 \leq x < 2,\\-x^2 + 5, x \geq 2,\end{cases}$当$x < 1$时,$f(x) = 0$;当$1 \leq x < 2$时,$f(x) = x + 1 \in [2, 3)$;当$x \geq 2$时,$f(x) = -x^2 + 5 \in (-\infty, 1]$;令$t = f(a)$,则由$f[f(a)] = 1$,得$f(t) = 1$,由上述分析可得$t \geq 2$且$-t^2 + 5 = 1$,解得$t = 2$,即$f(a) = 2$,所以$1 \leq a < 2$且$a + 1 = 2$,解得$a = 1$。
12. 【题型一、三】函数$f(x)=\begin{cases}x^2 - 4x + 3,0\leq x\leq3,\\x + 3,-3\leq x < 0\end{cases}$的值域为(
A.$[-1,+\infty)$
B.$[3,+\infty)$
C.$[-1,0]$
D.$[-1,3]$
D
)A.$[-1,+\infty)$
B.$[3,+\infty)$
C.$[-1,0]$
D.$[-1,3]$
答案:
12.D【详解】方法一:因为$y = x^2 - 4x + 3 = (x - 2)^2 - 1$且$0 \leq x \leq 3$,所以当$x = 2$时,$y_{min} = -1$,当$x = 0$时,$y_{max} = 3$;当$-3 \leq x < 0$时,$0 \leq x + 3 < 3$,所以函数$f(x) = \begin{cases}x^2 - 4x + 3, 0 \leq x \leq 3,\\x + 3, -3 \leq x < 0\end{cases}$的最小值为-1,最大值为3,故函数$f(x)$的值域为$[-1, 3]$。方法二:画出$f(x)$的草图,如图,由图象可知函数$f(x)$的最小值为-1,最大值为3,故函数$f(x)$的值域为$[-1, 3]$。
13. 【题型一、三】(2025·上海阶段练习)设$m\in R$,已知$f(x)=\begin{cases}x^2,x < 1,\\x + 1,x\geq1,\end{cases}$若$f(m) < 1$,则$m$的取值范围为
(-1, 1)
。
答案:
13.$(-1, 1)$【详解】当$m < 1$时,$m^2 < 1$,解得$-1 < m < 1$,因此$-1 < m < 1$;当$m \geq 1$时,$m + 1 < 1$,解得$m < 0$,无解,所以$m$的取值范围为$(-1, 1)$。
14. 【题型一、二、三】(2025·上海长宁期末)已知$\min\{a,b\}=\begin{cases}a,a < b,\\b,a\geq b,\end{cases}$则函数$f(x)=\min\{x + 1,-x^2 - 4x - 5\}$的值域为
(-\infty, -1]
。
答案:
14.$(-\infty, -1]$【详解】令$x + 1 = -x^2 - 4x - 5$,解得$x = -2$或$x = -3$,函数大致图象如图。由图可知,函数$f(x) \leq -1$。
查看更多完整答案,请扫码查看


