《2026年零差错高中数学必修第一册人教版》

5. 【题型一】（2025·广东领航高中联盟联合考试）已知某个店铺销售的某商品价格为$40$元/件，购物节期间这家店铺对该商品进行促销，顾客支付款不超过$100$元的部分按照$20\%$返现，超过$100$元的部分按照$30\%$返现。若促销活动期间在该店铺购买$x(x\in N^{*})$件商品，所需费用（支付款减去返现）为$f(x)$元，则$x\geqslant 3$时，$f(x)=$$28x + 10$。

答案： 5.$28x + 10$　[详解]因为当$x \geq 3$时，$40x \geq 3 × 40 = 120$，所以$f(x)=100 × 0.8+(40x - 100) × 0.7 = 28x + 10$.

6. 【题型一】某辆汽车以$xkm/h$的速度在高速公路上匀速行驶（考虑到高速公路行车安全，要求$60\leqslant x\leqslant 120$）时，每小时的油耗（所需要的汽油量）为$\frac{1}{5}(x - k + \frac{4400}{x})L$，其中$k$为常数。若汽车以$110km/h$的速度行驶时，每小时的油耗为$13L$，欲使每小时的油耗不超过$11L$，则$x$的取值范围为$[60,92]$。（结果保留整数）

答案： 6.$[60,92]$　[详解]由$\frac{1}{5}(x - 85+\frac{4400}{x}) \leq 11$，所以$48 \leq x \leq 70 + 10\sqrt{5}$，故$60 \leq x \leq 92$.

7. 【题型一、五】如下表，网上购鞋常常看到这样一张脚的长度与鞋号的对照表，第一行可以理解为脚的长度，第二行是我们习惯称呼的“鞋号”。

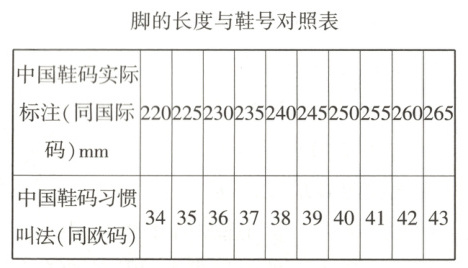
从上述表格中可以推算出$30$号的童鞋对应的脚的长度为$200mm$；若一个篮球运动员的脚长为$282mm$，则他该穿$47$号的鞋。

答案： 7.$200mm$ $47$　[详解]观察表格可知，习惯叫法=实际标注$×0.2 - 10$，故$30$号的童鞋对应的脚的长度为$200mm$，当脚长为$282mm$时，对应的习惯叫法为$282 × 0.2 - 10 = 46.4$，应穿$47$码的鞋.

8. 【题型一、二、五】某果园占地约$600$亩，拟选用果树$A$进行种植，在相同种植条件下，果树$A$每亩最多可种植$50$棵，种植成本$y$（万元）与果树数量$x$（百棵）之间的关系如下表所示。

(1) 根据上面表格中的数据判断$y = ax + b$与$y = c\sqrt{x} + d$哪一个更适合作为$y$与$x$的函数模型；
(2) 已知该果园的年利润$z$（万元）与$x$，$y$的关系为$z = 2y - 0.2x$，利用(1)中适合的模型估计果树数量$x$为多少时年利润最大。

答案： 8.解:
(1)①若选择$y = ax + b$作为$y$与$x$的函数模型，将$(1,1)$，$(4,4.4)$的坐标分别代入，得$\begin{cases}1 = a + b\\4.4 = 4a + b\end{cases}$，解得$\begin{cases}a = \frac{17}{15}\\b = - \frac{2}{15}\end{cases}$，所以$y = \frac{17}{15}x - \frac{2}{15}$.此时，当$x = 9$时，$y = \frac{151}{15} \approx 10.07$，与表格中的$7.8$相差较大，当$x = 16$时，$y = 18$，与表格中的$11.2$相差较大，所以$y = ax + b$不适合作为$y$与$x$的函数模型.
②若选择$y = c\sqrt{x}+d$作为$y$与$x$的函数模型，将$(1,1)$，$(4,4.4)$的坐标分别代入，得$\begin{cases}1 = c + d\\4.4 = 2c + d\end{cases}$，解得$\begin{cases}c = \frac{17}{5}\\d = - \frac{12}{5}\end{cases}$，所以$y = \frac{17}{5}\sqrt{x} - \frac{12}{5}$.当$x = 9$时，$y = \frac{39}{5}=7.8$，当$x = 16$时，$y = \frac{56}{5}=11.2$，$y$的值刚好与表格中的$7.8$和$11.2$相符合，所以$y = c\sqrt{x}+d$更适合作为$y$与$x$的函数模型.
(2)由题可知，该果园最多可种植$30000$棵该品种果树，所以$x$的取值范围为$[0,300]$，当$y = \frac{17}{5}\sqrt{x} - \frac{12}{5}$时，$z = 2y - 0.2x = \frac{34}{5}\sqrt{x} - \frac{24}{5} - \frac{1}{5}x = - \frac{1}{5}(\sqrt{x} - 17)^{2}+53$.易知，当$\sqrt{x}=17$，即$x = 289$时，$z$取最大值$53$(万元)，故果树数量为$289$百棵时，年利润最大.