《2026年易点通基础提分数学山西专版》

4. (2020·山西)竖直上抛物体离地面的高度$h$(m)与运动时间$t$(s)之间的关系可以近似地用公式$h=-5t^2 + v_0t + h_0$表示,其中$h_0$(m)是物体抛出时离地面的高度,$v_0$(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出,小球达到的离地面的最大高度为()

A.23.5m
B.22.5m
C.21.5m
D.20.5m

答案： 4. C

1. (2025·湖北)已知蓄电池的电压为定值,使用蓄电池时,电流$I$(单位:A)与电阻$R$(单位:Ω)是反比例函数关系,它的图象如图所示.当电阻$R$大于9Ω时,电流$I$可能是()

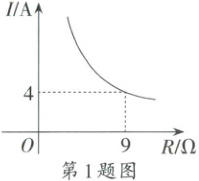
A.3A
B.4A
C.5A
D.6A

答案： 1. A

2. (2025·太原一模)随着科技的发展,智能照明系统普遍应用于人们的生活.在某种智能照明系统中,灯光亮度$y$与光敏传感器感应到的环境光线强度值$x$的关系,近似满足一次函数$y = kx + 100(k \neq 0)$,其中$0 ＜ x ＜ 1000$.已知当$x = 200$时,灯光亮度$y$的值为80,则当$x = 350$时,灯光亮度$y$的值为65.

答案： 2. 65

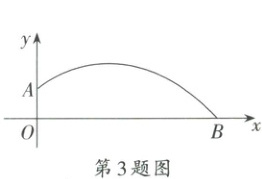
3. (2025·连云港)如图,小亮同学掷铅球时,铅球沿抛物线$y = a(x - 3)^2 + 2.5$运行,其中$x$是铅球离初始位置的水平距离,$y$是铅球离地面的高度.若铅球抛出时离地面的高度$OA$为1.6m,则铅球掷出的水平距离$OB$为8m.

答案： 3. 8

4. (2025·百校三)硬叶柳是杨柳科柳属直立灌木,在海拔4km到4.8km的高山环境下,其叶片长度$d$(mm)与海拔$h$(km)满足关系式:$d = 8h^2 - 72h + 182$.若$d = 20$mm,则硬叶柳生长的海拔$h$为$\frac{9}{2}$km.

答案： 4. $\frac{9}{2}$

5. 在物理学中,电磁波(又称电磁辐射)是由同相振荡且互相垂直的电场与磁场在空间中以波的形式移动,随着5G技术的发展,依靠电磁波作为信息载体的电子设备被广泛应用于民用及军事领域.电磁波的波长$\lambda$(单位:m)会随着电磁波的频率$f$(单位:MHz)的变化而变化.下表是某段电磁波在同种介质中,波长$\lambda$与频率$f$的部分对应值:

(1)该段电磁波的波长$\lambda$与频率$f$满足怎样的函数关系?并求出波长$\lambda$关于频率$f$的函数表达式;
(2)当$f = 50$MHz时,求此电磁波的波长$\lambda$.

答案： 5. 解：
(1)由表中数据可知，电磁波的波长$\lambda$与频率$f$的乘积为定值，
$\therefore$电磁波的波长$\lambda$与频率$f$满足反比例函数关系.
设波长$\lambda$关于频率$f$的函数表达式为$\lambda = \frac{k}{f}(k \neq 0)$.
把$(10, 30)$代入上式中，得$\frac{k}{10} = 30$，解，得$k = 300$.
$\therefore \lambda = \frac{300}{f}$.
(2)当$f = 50$时，$\lambda = \frac{300}{50} = 6$.
答：当$f = 50 MHz$时，此电磁波的波长$\lambda$为$6 m$.