2026年易点通基础提分数学山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年易点通基础提分数学山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
4. (2025·江苏扬州)如图,数轴上点$A$表示的数可能是 (
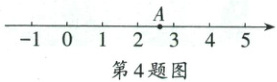
A.$\sqrt{2}$
B.$\sqrt{3}$
C.$\sqrt{7}$
D.$\sqrt{10}$
C
)
A.$\sqrt{2}$
B.$\sqrt{3}$
C.$\sqrt{7}$
D.$\sqrt{10}$
答案:
4.C
5. (2025·广东)计算$\sqrt{12} × \sqrt{3}$的结果是 (
A.$3$
B.$6$
C.$\sqrt{6}$
D.$2\sqrt{6}$
B
)A.$3$
B.$6$
C.$\sqrt{6}$
D.$2\sqrt{6}$
答案:
5.B
6. (2025·天津)估计$1 + \sqrt{6}$的值在 (
A.$1$和$2$之间
B.$2$和$3$之间
C.$3$和$4$之间
D.$4$和$5$之间
C
)A.$1$和$2$之间
B.$2$和$3$之间
C.$3$和$4$之间
D.$4$和$5$之间
答案:
6.C
7. (2025·学情调研卷)下列运算正确的是 (
A.$\sqrt{2} + \sqrt{3} = \sqrt{5}$
B.$\sqrt{2} × \sqrt{3} = \sqrt{6}$
C.$3\sqrt{2} - \sqrt{2} = 3$
D.$\sqrt{14} ÷ \sqrt{7} = 2$
B
)A.$\sqrt{2} + \sqrt{3} = \sqrt{5}$
B.$\sqrt{2} × \sqrt{3} = \sqrt{6}$
C.$3\sqrt{2} - \sqrt{2} = 3$
D.$\sqrt{14} ÷ \sqrt{7} = 2$
答案:
7.B
8. (2025·太原一模)计算$\sqrt{12} + \sqrt{3}$
$3\sqrt{3}$
$=$。
答案:
8.$3\sqrt{3}$
9. (2025·百校二)计算$(\sqrt{6} - \sqrt{2})(\sqrt{6} + \sqrt{2})$的结果是。
4
答案:
9.4
10. 计算:$2\sqrt{12} - 6\sqrt{\dfrac{1}{3}} + 3\sqrt{48}$。
答案:
10.解:原式$=4\sqrt{3}-2\sqrt{3}+12\sqrt{3}=14\sqrt{3}$.
11. 阅读与计算
请阅读以下材料,并完成相应的任务。
|斐波那契$(1175 - 1250)$是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果.在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.|
|斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第$n$个数可以用$\dfrac{1}{\sqrt{5}}\left[\left(\dfrac{1 + \sqrt{5}}{2}\right)^{n} - \left(\dfrac{1 - \sqrt{5}}{2}\right)^{n}\right]$表示(其中$n \geqslant 1$).这是用无理数表示有理数的一个范例.|
任务:请根据以上材料,通过计算求出斐波那契数列中的第$1$个数和第$2$个数。
请阅读以下材料,并完成相应的任务。
|斐波那契$(1175 - 1250)$是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果.在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.|
|斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第$n$个数可以用$\dfrac{1}{\sqrt{5}}\left[\left(\dfrac{1 + \sqrt{5}}{2}\right)^{n} - \left(\dfrac{1 - \sqrt{5}}{2}\right)^{n}\right]$表示(其中$n \geqslant 1$).这是用无理数表示有理数的一个范例.|
任务:请根据以上材料,通过计算求出斐波那契数列中的第$1$个数和第$2$个数。
答案:
11.解:第1个数:当$n = 1$时,
$\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)-\left(\frac{1-\sqrt{5}}{2}\right)\right]=\frac{1}{\sqrt{5}}\left[\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2}\right]=\frac{1}{\sqrt{5}}×\sqrt{5}=1$.
第2个数:当$n = 2$时,
$\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{2}-\left(\frac{1-\sqrt{5}}{2}\right)^{2}\right]=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)-\left(\frac{1-\sqrt{5}}{2}\right)\right]\left[\left(\frac{1+\sqrt{5}}{2}\right)+\left(\frac{1-\sqrt{5}}{2}\right)\right]=\frac{1}{\sqrt{5}}\left[\frac{1+\sqrt{5}}{2}+\frac{1-\sqrt{5}}{2}\right]\left[\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2}\right]=\frac{1}{\sqrt{5}}×1×\sqrt{5}=1$。
$\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)-\left(\frac{1-\sqrt{5}}{2}\right)\right]=\frac{1}{\sqrt{5}}\left[\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2}\right]=\frac{1}{\sqrt{5}}×\sqrt{5}=1$.
第2个数:当$n = 2$时,
$\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{2}-\left(\frac{1-\sqrt{5}}{2}\right)^{2}\right]=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)-\left(\frac{1-\sqrt{5}}{2}\right)\right]\left[\left(\frac{1+\sqrt{5}}{2}\right)+\left(\frac{1-\sqrt{5}}{2}\right)\right]=\frac{1}{\sqrt{5}}\left[\frac{1+\sqrt{5}}{2}+\frac{1-\sqrt{5}}{2}\right]\left[\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2}\right]=\frac{1}{\sqrt{5}}×1×\sqrt{5}=1$。
查看更多完整答案,请扫码查看


