《2026年点金训练精讲巧练高中数学选择性必修第二册人教A版》

知识点一 判断函数 $ y = f(x) $ 的单调性的步骤
第1步，确定函数的定义域；
第2步，求出导数 $ f'(x) $ 的零点；
第3步，用 $ f'(x) $ 的零点将 $ f(x) $ 的定义域划分为若干个区间，列表给出 $ f'(x) $ 在各区间上的正负，由此得出函数 $ y = f(x) $ 在定义域内的单调性.

答案： 知识点一 定义域 零点 正负

一般地，设函数 $ y = f(x) $，在区间 $ (a,b) $ 上：

答案： 知识点二 较快 陡峭 较慢 平缓

1. 判断正误(正确的打“√”，错误的打“×”).
(1)利用导数求函数的单调区间时，要先确定函数的定义域. (√)
(2)如图，函数 $ y = f(x) $ 的图象在 $ (0,a) $ 内“陡峭”，在 $ (a,+\infty) $ 上“平缓”. (√)
(3)函数 $ y = ax^3 - 1(a\in\mathbf{R}) $ 在 $ \mathbf{R} $ 上单调递增. (×)

答案： 1.
(1)√
(2)√
(3)× 提示：$y^{\prime}=3ax^{2}$.当$a＞0$时，$y^{\prime} \geqslant 0$，仅在$x=0$时$y^{\prime}=0$，所以函数在$\mathbf{R}$上单调递增；当$a＜0$时，$y^{\prime} \leqslant 0$，仅在$x=0$时$y^{\prime}=0$，所以函数在$\mathbf{R}$上单调递减；当$a=0$时，$y^{\prime}=0$，函数在$\mathbf{R}$上不具备单调性.

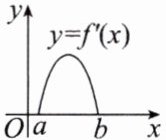
2. 已知 $ f'(x) $ 是 $ f(x) $ 的导函数，$ f'(x) $ 的图象如图所示，则 $ f(x) $ 的图象只可能是(D)

答案： 2.D 解析：从$f^{\prime}(x)$的图象可以看出，在区间$(a,b)$上，$f^{\prime}(x)$先增后减，所以$f(x)$的图象先越来越陡，之后越来越平缓，只有选项D符合.

3. 请思考并回答下列问题：
(1)若在某区间上有有限个点使 $ f'(x) = 0 $，其余的点恒有 $ f'(x) ＞ 0 $，则 $ f(x) $ 仍单调递增吗？
(2)可导函数 $ f(x) $ 在区间 $ (a,b) $ 上单调递增的充要条件是什么？

答案： 3.
(1)提示：$f(x)$仍单调递增(单调递减的情形类似).
(2)提示：可导函数$f(x)$在区间$(a,b)$上单调递增的充要条件是对任意的$x \in (a,b)$，都有$f^{\prime}(x) \geqslant 0$，且在$(a,b)$的任一非空子区间上$f^{\prime}(x)$不恒为0.