《2025年核心素养学练评七年级数学上册人教版》

21. （8 分）小华输液前发现瓶中药液共 250 毫升，输液器包装袋上标有“15 滴/毫升”的字样. 输液开始时，药液流速为 75 滴/分钟. 小华感觉身体不适，输液 10 分钟时调整了药液流速，输液 20 分钟时，瓶中的药液余量为 160 毫升.
（1）求输液 10 分钟时瓶中的药液余量；
（2）求小华从输液开始到结束所需的时间.

答案： 解:
(1)250-75÷15×10=250-50=200(毫升).答:输液10分钟时瓶中的药液余量是200毫升.
(2)设小华从输液开始到结束所需的时间为t分钟,依题意得$\frac{200-160}{20-10}(t-20)=160$,解得t=60.答:小华从输液开始到结束所需的时间为60分钟.

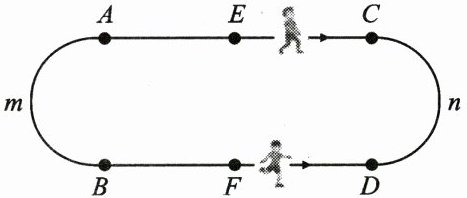
22. （10 分）【综合与实践】如图，这是某校园内的环形跑道，跑道是由线段 $ AC $、$ BD $ 及半圆 $ m $、$ n $ 组成的. 已知跑道的周长为 400 m，半圆 $ m $、$ n $ 的长都为 88 m，$ AC = BD $，$ E $ 和 $ F $ 分别是线段 $ AC $ 和 $ BD $ 的中点. （请用方程的相关知识解决下列问题）
（1）求线段 $ AE $ 的长；
（2）小明和小英在如图所示的环形跑道上练习跑步，已知小明、小英两人分别从点 $ E $、$ F $ 两处同时沿着箭头方向出发，小明的速度是 6 m/s，小英的速度是 4 m/s.
①多长时间后，两人首次相遇？
②在第二次相遇前，经过多长时间两人在跑道上相距 100 m？

答案： 解:
(1)AC=BD=(400-88×2)÷2=112(m).因为E是线段AC的中点,所以AE=$\frac{1}{2}$AC=56m.答:线段AE的长为56m.
(2)①设x s后,两人首次相遇.根据题意得(6+4)x=$\frac{1}{2}$×400,解得x=20.答:20s后,两人首次相遇.②设在第二次相遇前,经过y s两人在跑道上相距100m.根据题意得(6+4)y-$\frac{1}{2}$×400=100或(6+4)y-$\frac{1}{2}$×400=400-100,解得y=30或y=50.答:在第二次相遇前,经过30s或50s两人在跑道上相距100m.

23. （11 分）某班组织庆祝元旦知识竞赛，共设有 20 道选择题，各题分值相同，每题必答. 下表记录了 5 位参赛者的得分情况，根据表中信息回答下列问题：

（1）这次竞赛中答对一题得5分，答错一题扣________1分；
（2）参赛者 $ F $ 的得分为 82 分，求他答错了几道题？
（3）参赛者 $ G $ 说他的得分为 75 分，你认为可能吗？请说明理由.

答案： 解:
(1)由题意得,这次竞赛中答对一题的得分是100÷20=5(分),答错一题的扣分为19×5-94=1(分).故答案为5;1.
(2)设参赛者F答对了x道题,则答错了(20-x)道题.由题意得5x-(20-x)=82,解得x=17,所以20-x=20-17=3.答:参赛者F答错了3道题.
(3)不可能.理由:假设他得75分,设答对了y道题,则答错了(20-y)道题.由题意得5y-(20-y)=75,解得y=$\frac{95}{6}$.又因为y为整数,所以参赛者G说他得75分是不可能的.