第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
19. (8 分)如图,在同一个平面内有四个点,请用直尺和圆规按下列要求作图(不写作图步骤,保留作图痕迹,而且要求作图时先使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑):
(1)作射线 AB;
(2)作直线 AC 与直线 BD 相交于点 O;
(3)在射线 AB 上作线段 $ AC' $,使 $ AC' = AC $.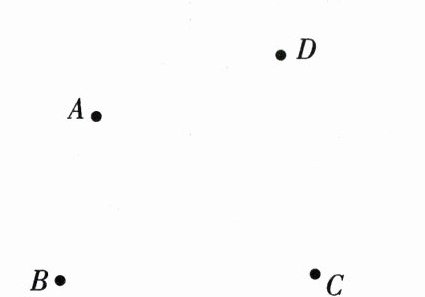
(1)作射线 AB;
(2)作直线 AC 与直线 BD 相交于点 O;
(3)在射线 AB 上作线段 $ AC' $,使 $ AC' = AC $.

答案:
解:
(1)射线AB如图所示.
(2)直线AC与直线BD相交于点O如图所示.
(3)作法:以A为圆心,线段AC的长为半径,在射线AB上画弧,交射线AB于C',则线段AC'即为所求.

解:
(1)射线AB如图所示.
(2)直线AC与直线BD相交于点O如图所示.
(3)作法:以A为圆心,线段AC的长为半径,在射线AB上画弧,交射线AB于C',则线段AC'即为所求.

20. (8 分)计算:
(1)$ 45^{\circ}10' - 21^{\circ}35'20'' $;
(2)$ 42^{\circ}16' + 18^{\circ}23' × 2 $;
(3)$ 90^{\circ} - (23^{\circ}16' + 17^{\circ}23') $;
(4)$ 80^{\circ}40' ÷ 6 - 10^{\circ}37'52'' $.
(1)$ 45^{\circ}10' - 21^{\circ}35'20'' $;
(2)$ 42^{\circ}16' + 18^{\circ}23' × 2 $;
(3)$ 90^{\circ} - (23^{\circ}16' + 17^{\circ}23') $;
(4)$ 80^{\circ}40' ÷ 6 - 10^{\circ}37'52'' $.
答案:
解:
(1)原式=23°34'40''.
(2)原式=79°2'.
(3)原式=49°21'.
(4)原式=2°48'48''.
(1)原式=23°34'40''.
(2)原式=79°2'.
(3)原式=49°21'.
(4)原式=2°48'48''.
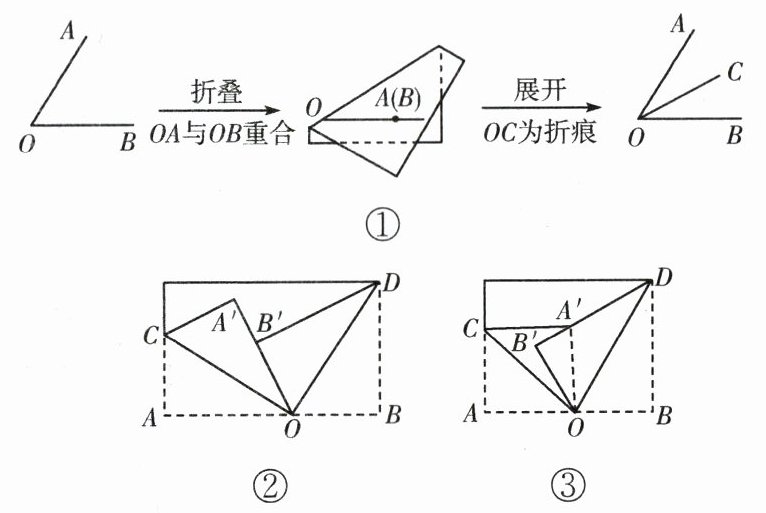
21. (8 分)(教材变式)利用折纸可以作出角平分线. 如图①,通过折叠、展开,则 OC 为 $ \angle AOB $ 的平分线. 折叠长方形纸片,OC,OD 均是折痕,折叠后,点 A 落在点 $ A' $ 处,点 B 落在点 $ B' $ 处.
(1)如图②,当点 $ B' $ 在 $ OA' $ 上时,判断 $ \angle AOC $ 与 $ \angle BOD $ 的关系,并说明理由;
(2)如图③,当点 $ B' $ 在 $ \angle COA' $ 的内部时,若 $ \angle AOC = 44^{\circ} $,$ \angle BOD = 61^{\circ} $,求 $ \angle A'OB' $ 的度数.
(1)如图②,当点 $ B' $ 在 $ OA' $ 上时,判断 $ \angle AOC $ 与 $ \angle BOD $ 的关系,并说明理由;
(2)如图③,当点 $ B' $ 在 $ \angle COA' $ 的内部时,若 $ \angle AOC = 44^{\circ} $,$ \angle BOD = 61^{\circ} $,求 $ \angle A'OB' $ 的度数.

答案:
解:
(1)∠AOC与∠BOD的关系是∠AOC+∠BOD=90°.理由:由折叠的性质可知∠AOC=∠A'OC,∠BOD=∠B'OD,因为∠AOC+∠A'OC+∠BOD+∠B'OD=180°,所以2∠AOC+2∠BOD=180°,所以∠AOC+∠BOD=90°.
(2)由折叠的性质可知∠AOC=∠A'OC,∠BOD=∠B'OD,所以∠AOA'=2∠AOC,∠BOB'=2∠BOD,因为∠AOC=44°,∠BOD=61°,所以∠AOA'=88°,∠BOB'=122°,所以∠A'OB'=∠AOA'+∠BOB'-180°=88°+122°-180°=30°.
(1)∠AOC与∠BOD的关系是∠AOC+∠BOD=90°.理由:由折叠的性质可知∠AOC=∠A'OC,∠BOD=∠B'OD,因为∠AOC+∠A'OC+∠BOD+∠B'OD=180°,所以2∠AOC+2∠BOD=180°,所以∠AOC+∠BOD=90°.
(2)由折叠的性质可知∠AOC=∠A'OC,∠BOD=∠B'OD,所以∠AOA'=2∠AOC,∠BOB'=2∠BOD,因为∠AOC=44°,∠BOD=61°,所以∠AOA'=88°,∠BOB'=122°,所以∠A'OB'=∠AOA'+∠BOB'-180°=88°+122°-180°=30°.
查看更多完整答案,请扫码查看


