《2025年核心素养学练评七年级数学上册人教版》

21.(8 分)从一个边长为 $a$ 的正方形纸片(如图 1)上剪去两个相同的小长方形,得到一个美术字“S”的图案(如图 2),再将剪下的两个小长方形拼成一个新长方形(如图 3).

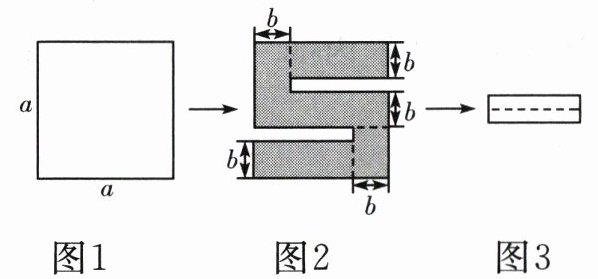
(1)用含有 $a,b$ 的式子表示新长方形的长是a-b,宽是a-3b；
(2)若 $a = 8$,剪去的 1 个小长方形的宽为 1,求新长方形的周长.
由题意,得a-3b=2.因为a=8,所以b=2.当a=8,b=2时,新长方形的周长=2[(a-b)+(a-3b)]=4a-8b=16.

答案：
(1)a-b;a-3b
(2)由题意,得a-3b=2.因为a=8,所以b=2.当a=8,b=2时,新长方形的周长=2[(a-b)+(a-3b)]=4a-8b=16.

22.(10 分)(新考法)学习了“整式的加减”这节课后,李老师设计了一个小游戏：已知 $X,Y$ 两个多项式,$X = mx^{2}+2x - 3,Y = 4x^{2}-nx + 2$,其中 $m,n$ 为有理数,请同学们为 $m,n$ 选择一组喜欢的数值代入,并计算出 $X - Y$ 的值,大家兴致高涨,积极参与.
(1)小明选择了一组数值,发现计算的结果是一个常数,请你求出他所选择的 $m,n$ 的值；
(2)小亮选择了另一组数值,在计算的过程中,误将 $Y$ 多项式中的“$-$”看成了“$+$”,得出的结果为 $-2x^{2}+x - 5$,请你帮小亮计算出正确的结果.

答案：
(1)因为X=m$x^{2}$+2x-3,Y=4$x^{2}$-nx+2,所以X-Y=(m$x^{2}$+2x-3)-(4$x^{2}$-nx+2)=m$x^{2}$+2x-3-4$x^{2}$+nx-2=(m-4)$x^{2}$+(2+n)x-5,因为计算的结果是一个常数,所以m-4=0,2+n=0,所以m=4,n=-2.
(2)由题意得(m$x^{2}$+2x-3)-(4$x^{2}$+nx+2)=m$x^{2}$+2x-3-4$x^{2}$-nx-2=(m-4)$x^{2}$+(2-n)x-5,因为得出的结果为-2$x^{2}$+x-5,所以m-4=-2,2-n=1,所以m=2,n=1,所以X-Y=2$x^{2}$+2x-3-4$x^{2}$+x-2=-2$x^{2}$+3x-5,所以正确的结果为-2$x^{2}$+3x-5.