第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
18. (6 分)已知$∠AOB = 50^{\circ}$,$∠AOC = \dfrac{1}{2}∠AOB$,反向延长$OC$至$D$。请用半圆仪(量角器)和直尺画出图形,并求$∠BOD$的度数。
答案:
解:画出图形,分两种情况,如图1、图2.


因为∠AOC=$\frac{1}{2}$∠AOB,
所以如图1,∠BOC=∠AOB−∠AOC=∠AOB−$\frac{1}{2}$∠AOB=
$\frac{1}{2}$∠AOB=25°.
所以∠BOD=180°−∠BOC=180°−25°=155°.
如图2,∠BOC=∠AOB+∠AOC=$\frac{3}{2}$∠AOB=75°,
所以∠BOD=180°−∠BOC=180°−75°=105°.
综上所述,∠BOD的度数是155°或105°.
解:画出图形,分两种情况,如图1、图2.


因为∠AOC=$\frac{1}{2}$∠AOB,
所以如图1,∠BOC=∠AOB−∠AOC=∠AOB−$\frac{1}{2}$∠AOB=
$\frac{1}{2}$∠AOB=25°.
所以∠BOD=180°−∠BOC=180°−25°=155°.
如图2,∠BOC=∠AOB+∠AOC=$\frac{3}{2}$∠AOB=75°,
所以∠BOD=180°−∠BOC=180°−75°=105°.
综上所述,∠BOD的度数是155°或105°.
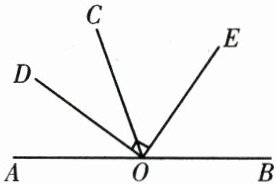
19. (8 分)如图,$O$为直线$AB$上一点,$∠AOC = 70^{\circ}$,$OD$是$∠AOC$的平分线,$∠DOE = 90^{\circ}$。
(1)图中小于平角的角的个数是
(2)求$∠BOD$的度数;
(3)猜想$OE$是否平分$∠BOC$?并说明理由。
(1)图中小于平角的角的个数是
9
;(2)求$∠BOD$的度数;
(3)猜想$OE$是否平分$∠BOC$?并说明理由。

答案:
解:
(1)小于平角的角有∠AOD,∠DOC,∠COE,
∠EOB,∠AOC,∠AOE,∠DOE,∠DOB,∠COB,
共9个.故答案为9.
(2)因为∠AOC=70°,OD是∠AOC的平分线,
所以∠AOD=∠COD=$\frac{1}{2}$∠AOC=35°.
所以∠BOD=180°−∠AOD=180°−35°=145°.
(3)OE平分∠BOC.理由如下:
因为∠DOE=90°,
所以∠BOE=∠BOD−∠DOE=145°−90°=55°,
∠COE=∠DOE−∠COD=90°−35°=55°,
所以∠BOE=∠COE,所以OE平分∠BOC.
(1)小于平角的角有∠AOD,∠DOC,∠COE,
∠EOB,∠AOC,∠AOE,∠DOE,∠DOB,∠COB,
共9个.故答案为9.
(2)因为∠AOC=70°,OD是∠AOC的平分线,
所以∠AOD=∠COD=$\frac{1}{2}$∠AOC=35°.
所以∠BOD=180°−∠AOD=180°−35°=145°.
(3)OE平分∠BOC.理由如下:
因为∠DOE=90°,
所以∠BOE=∠BOD−∠DOE=145°−90°=55°,
∠COE=∠DOE−∠COD=90°−35°=55°,
所以∠BOE=∠COE,所以OE平分∠BOC.
20. (8 分)给出如下定义:如果$∠AOC + ∠BOC = 90^{\circ}$,且$∠AOC = k∠BOC$($k$为正整数),那么称$∠AOC$是$∠BOC$的“倍锐角”。
(1)下列三个条件中,能判定$∠AOC$是$∠BOC$的“倍锐角”的是________(填写序号)。
①$∠BOC = 15^{\circ}$;②$∠AOC = 70^{\circ}$;③$OC$是$∠AOB$的平分线。
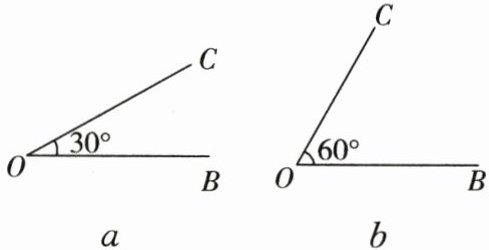
(2)如图$a$,当$∠BOC = 30^{\circ}$时,在图中画出$∠BOC$的一个“倍锐角”$∠AOC$。
(3)如图$b$,当$∠BOC = 60^{\circ}$时,射线$OB$绕点$O$旋转,每次旋转$10^{\circ}$,则它的“倍锐角”$∠AOC =$________。
(4)当$∠BOC = m^{\circ}$,且存在它的“倍锐角”$∠AOC$时,求$∠AOB$的度数。
(1)下列三个条件中,能判定$∠AOC$是$∠BOC$的“倍锐角”的是________(填写序号)。
①$∠BOC = 15^{\circ}$;②$∠AOC = 70^{\circ}$;③$OC$是$∠AOB$的平分线。
(2)如图$a$,当$∠BOC = 30^{\circ}$时,在图中画出$∠BOC$的一个“倍锐角”$∠AOC$。
(3)如图$b$,当$∠BOC = 60^{\circ}$时,射线$OB$绕点$O$旋转,每次旋转$10^{\circ}$,则它的“倍锐角”$∠AOC =$________。
(4)当$∠BOC = m^{\circ}$,且存在它的“倍锐角”$∠AOC$时,求$∠AOB$的度数。

答案:
解:
(1)①③.
(2)若∠BOC=30°,∠AOC+∠BOC=90°,则∠AOC=60°=
2∠BOC,有以下两种情况(任选其一即可).

(3)80°或60°.
解析:因为∠BOC=60°,且射线OB绕点O每次旋转10°,
所以∠BOC度数的取值有0°,10°,20°,30°,40°,50°,60°,70°,
80°,90°这几种,对每个可能的值进行分析可知,只有两种情况下,∠AOC是∠BOC的“倍锐角”:
①当∠BOC=10°时,∠AOC=80°=8∠BOC;
②当∠BOC=30°时,∠AOC=60°=2∠BOC.
所以∠AOC=80°或60°.
(4)若∠BOC存在它的“倍锐角”∠AOC,则有两种情况:
①如图1,当OA在OC的上方时,∠AOB=∠AOC+∠BOC=90°;


②如图2,当OA在OC的下方时,∠AOB=∠AOC一∠BOC=
90°−∠BOC−∠BOC=(90−2m)°.
所以∠AOB=90°或(90−2m)°.
解:
(1)①③.
(2)若∠BOC=30°,∠AOC+∠BOC=90°,则∠AOC=60°=
2∠BOC,有以下两种情况(任选其一即可).

(3)80°或60°.
解析:因为∠BOC=60°,且射线OB绕点O每次旋转10°,
所以∠BOC度数的取值有0°,10°,20°,30°,40°,50°,60°,70°,
80°,90°这几种,对每个可能的值进行分析可知,只有两种情况下,∠AOC是∠BOC的“倍锐角”:
①当∠BOC=10°时,∠AOC=80°=8∠BOC;
②当∠BOC=30°时,∠AOC=60°=2∠BOC.
所以∠AOC=80°或60°.
(4)若∠BOC存在它的“倍锐角”∠AOC,则有两种情况:
①如图1,当OA在OC的上方时,∠AOB=∠AOC+∠BOC=90°;


②如图2,当OA在OC的下方时,∠AOB=∠AOC一∠BOC=
90°−∠BOC−∠BOC=(90−2m)°.
所以∠AOB=90°或(90−2m)°.
查看更多完整答案,请扫码查看


