第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
7. 如图,OA 的方向是北偏东 $ 15^{\circ} $,OB 的方向是西北方向. 若 $ \angle AOC = \angle AOB $,则 OC 的方向是(
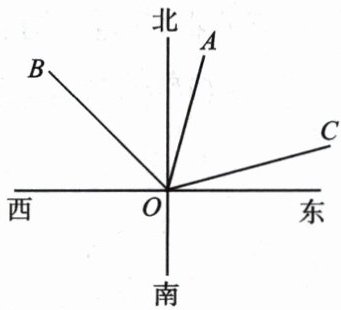
A.北偏东 $ 75^{\circ} $
B.北偏东 $ 60^{\circ} $
C.北偏东 $ 80^{\circ} $
D.北偏东 $ 65^{\circ} $
A
)
A.北偏东 $ 75^{\circ} $
B.北偏东 $ 60^{\circ} $
C.北偏东 $ 80^{\circ} $
D.北偏东 $ 65^{\circ} $
答案:
A
8. 已知 $ \angle \alpha $ 是锐角,$ \angle \alpha $ 与 $ \angle \beta $ 互补,$ \angle \alpha $ 与 $ \angle \gamma $ 互余,则 $ \angle \beta - \angle \gamma $ 等于(
A.$ 180^{\circ} $
B.$ 90^{\circ} $
C.$ 45^{\circ} $
D.无法确定
B
)A.$ 180^{\circ} $
B.$ 90^{\circ} $
C.$ 45^{\circ} $
D.无法确定
答案:
B 解析:因为∠α是锐角,∠α与∠β互补,∠α与∠γ互余,所以∠α+∠β=180°,∠α+∠γ=90°,所以∠β=180°−∠α,∠γ=90°−∠α,所以∠β−∠γ=180°−∠α−(90°−∠α)=90°.故选B.
9. 如图,$ \angle AOC = 90^{\circ} $,$ \angle COB = \alpha $,OD 平分 $ \angle AOB $,则 $ \angle COD $ 的度数为(
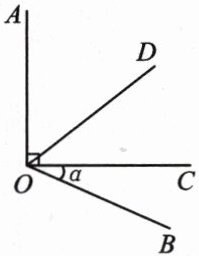
A.$ \frac{\alpha}{2} $
B.$ 45^{\circ} - \frac{\alpha}{2} $
C.$ 45^{\circ} - \alpha $
D.$ 90^{\circ} - \alpha $
B
)
A.$ \frac{\alpha}{2} $
B.$ 45^{\circ} - \frac{\alpha}{2} $
C.$ 45^{\circ} - \alpha $
D.$ 90^{\circ} - \alpha $
答案:
B 解析:因为∠AOC=90°,∠BOC=α,所以∠AOB=90°+α.因为OD平分∠AOB,所以∠BOD=$\frac{1}{2}$∠AOB=45°+$\frac{\alpha}{2}$.所以∠COD=∠BOD−∠BOC=45°+$\frac{\alpha}{2}$−α=45°−$\frac{\alpha}{2}$.故选B.
10. 如图,已知 $ \angle AOB = 180^{\circ} $,$ \angle AOC = 110^{\circ} $,现将射线 OA 绕点 O 顺时针匀速旋转,射线 OB 保持不动,当射线 OA 与射线 OB 重合时停止旋转. 当三条射线构成的角中有两个角相等(重合除外)时,射线 OA 旋转的角度为(
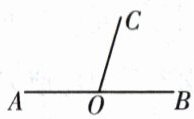
A.$ 40^{\circ} $
B.$ 60^{\circ} $
C.$ 40^{\circ} $ 或 $ 145^{\circ} $
D.$ 60^{\circ} $ 或 $ 150^{\circ} $
C
)
A.$ 40^{\circ} $
B.$ 60^{\circ} $
C.$ 40^{\circ} $ 或 $ 145^{\circ} $
D.$ 60^{\circ} $ 或 $ 150^{\circ} $
答案:
C 解析:经分析,三条射线构成的角中有两个角相等(重合除外)时,可能存在以下两种情形:①当射线OA旋转到∠BOC 的外部时,∠AOC=∠BOC=70°,此时射线OA旋转的角度为110°−70°=40°.②当射线OA旋转到∠BOC内部时,∠AOC=∠AOB,此时∠AOB=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×(180°−110°)=35°,此时射线OA旋转的角度为180°−35°=145°.综上,射线OA旋转的角度为40°或145°.故选C.
11. 老师在黑板上用粉笔画出了一个太阳,为了把太阳快速涂成红色,把粉笔平放在黑板上转动,其中蕴含的数学知识是
线动成面
.
答案:
线动成面
12. 用棱长为 1 的小正方体摆成如图所示的几何体,从上面看这个几何体,看到的平面图形的面积是
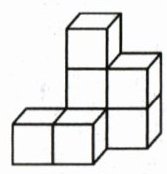
4
.
答案:
4
13. 如图,已知线段 AB 上有 C,D 两点,且 $ AC:CD:DB = 2:3:4 $,E,F 分别为 AC,DB 的中点,$ EF = 2.4 cm $,则 $ AB = $
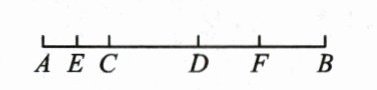
3.6cm
.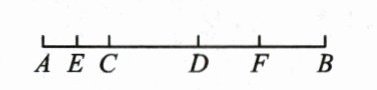
答案:
3.6cm
14. 如图,在 $ \angle AOB $ 内,从顶点 O 画一条射线,图中共有______个角;若从顶点 O 画 10 条射线,图中共有______个角.

答案:
3 66 解析:由题图得,从顶点O画一条射线,则此时题图中共有3条射线,有1+2=$\frac{3×2}{2}$=3(个)角.当在∠AOB内再添加一条射线,如图,则此时图中共有4条射线,有1+2+3=$\frac{4×3}{2}$=6(个)角,……,所以,若从顶点O画10条射线,则图中一共有10+2=12(条)射线,有1+2+3+..+11=$\frac{12×11}{2}$=66(个)角.故答案为3;66.

3 66 解析:由题图得,从顶点O画一条射线,则此时题图中共有3条射线,有1+2=$\frac{3×2}{2}$=3(个)角.当在∠AOB内再添加一条射线,如图,则此时图中共有4条射线,有1+2+3=$\frac{4×3}{2}$=6(个)角,……,所以,若从顶点O画10条射线,则图中一共有10+2=12(条)射线,有1+2+3+..+11=$\frac{12×11}{2}$=66(个)角.故答案为3;66.

查看更多完整答案,请扫码查看


