《2025年核心素养学练评七年级数学上册人教版》

23. （11 分）如图，点$O$为原点，点$A$表示的数为 1，点$B$表示的数为$-3$。
（1）若点$P$在数轴上，且$PA + PB = 6$，求点$P$表示的数；
（2）若点$M$在数轴上，且$MA:MB = 1:3$，求点$M$表示的数；
（3）若点$A$的速度为 5 个单位长度/秒，点$B$的速度为 2 个单位长度/秒，点$O$的速度为 1 个单位长度/秒，$A$，$B$，$O$同时向右运动，则多少秒后，$O$恰好为线段$AB$的中点？

答案： 解:
(1)①当点P在A,B之间时，不合题意，舍去;
②当点P在点A右边时，点P表示的数为2;
③当点P在点B左边时，点P表示的数为−4.
综上所述，点P表示的数为2或−4.
(2)①当点M在线段AB上时，点M表示的数为0;
②当点M在线段BA的延长线上时，点M表示的数为3;
③当点M在线段AB的延长线上时，不合题意，舍去.
综上所述，点M表示的数为0或3.
(3)设x秒后，点B运动到点B'，点A运动到点A'，点O运动到点O',此时O'A'=O'B',点A',B'在点O'两侧,
则BB'=2x,OO'=x,AA'=5x,所以点B'表示的数为2x−3,点O'表示的数为x,点A'表示的数为5x+1.
所以O'A'=5x+1−x=4x+1,O'B'=x−(2x−3)=3−x,所以4x+1=3−x,解得x=0.4,
故0.4秒后，O恰好为线段AB的中点.

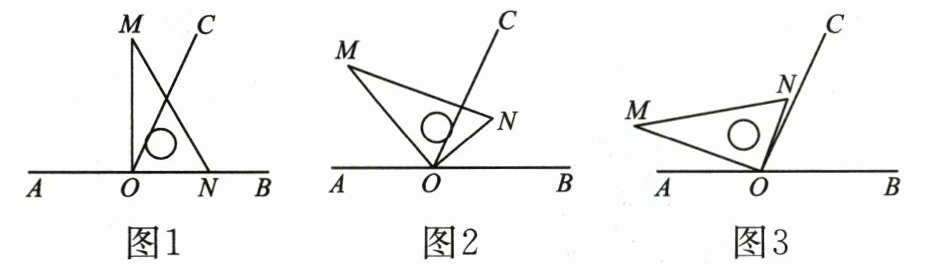
24. （12 分）点$O$为直线$AB$上的一点，过点$O$作射线$OC$，使$∠BOC = 65^{\circ}$，将一直角三角板的直角顶点放在点$O$处。
（1）如图 1，当直角三角板$MON$的一边$ON$与射线$OB$重合时，$∠MOC =$25°；
（2）如图 2，将直角三角板$MON$绕点$O$逆时针旋转一定角度，此时$OC$是$∠MOB$的平分线，求$∠AOM$和$∠CON$的度数；
（3）将直角三角板$MON$绕点$O$逆时针旋转至图 3 所示的位置时，$∠AOM = 4∠NOC$，求$∠NOB$的度数。

答案： 解:
(1)25°.
(2)因为∠BOC=65°,OC是∠MOB的平分线，
所以∠MOB=2∠BOC=130°,∠MOC=∠BOC=65°.
所以∠AOM=180°−∠MOB=180°−130°=50°,
∠CON=∠MON−∠MOC=90°−65°=25°.
(3)因为∠AOM+∠MON+∠NOC+∠BOC=180°,
∠BOC=65°,∠MON=90°,
所以∠AOM+∠NOC=180°−65°−90°=25°.
因为∠AOM=4∠NOC,
所以∠NOC=5°.
所以∠NOB=∠NOC+∠BOC=5°+65°=70°.