《2025年核心素养学练评七年级数学上册人教版》

23. (11 分)根据如图所示的数轴,解答下面的问题：

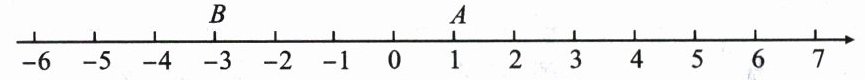
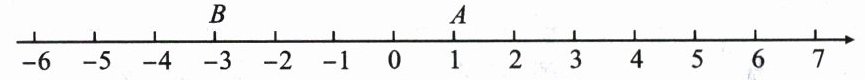
(1)点$A$表示的数是1,点$B$表示的数是-3；若将数轴折叠,使得点$A与-5$对应的点重合,则点$B$与数-1对应的点重合；
(2)观察数轴,与点$A$的距离为 4 的点表示的数是-3或5；
(3)已知点$M到A$,$B$两点的距离之和为 8,求点$M$表示的数.
(3)设点M表示的数是x.当点M在点A右边时,x-(-3)+x-1=8,解得x=3;当点M在点B左边时,(-3)-x+1-x=8,解得x=-5.所以点M表示的数为3或-5.

答案：
(1)1;-3;-1.
(2)-3或5.
(3)设点M表示的数是x.当点M在点A右边时,x-(-3)+x-1=8,解得x=3;当点M在点B左边时,(-3)-x+1-x=8,解得x=-5.所以点M表示的数为3或-5.

24. (12 分)(探究性问题)【观察】
(1)填空：$-\frac{1}{3}×(1×2×3 - 0×1×2) = $-2.
$-\frac{1}{3}×(2×3×4 - 1×2×3) = $-6.
$-\frac{1}{3}×(3×4×5 - 2×3×4) = $-12.
【猜想】
(2)写出(1)中的规律.
【迁移】
(3)解答以下两个问题：
① $-1×2 + (-2)×3 + (-3)×4 + … + (-n)×(n + 1) = $$-\frac{1}{3}n(n+1)(n+2)$.(用含有$n$的式子表示)
② $-\frac{1}{3}×(1×2×3 - 0×1×2) + (-\frac{1}{3})×(2×3×4 - 1×2×3) + … + (-\frac{1}{3})×(7×8×9 - 6×7×8) = $-168.

答案：
(1)-2;-6;-12.
(2)规律为$-\frac{1}{3}$×[n(n+1)(n+2)-n(n-1)(n+1)]=-n(n+1).
(3)①$-\frac{1}{3}$n(n+1)(n+2);②-168.