第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
21. (8 分)已知$C$,$D$,$E$分别为线段$AB$上的点(点$D$在点$E$左边),且满足$DE = \dfrac{1}{2}AB$。
(1)如图,若$BC = 2AC$,$AB = 9$,$D$为$AC$的中点时,求$BE$的长;
(2)若$C$为$BE$的中点,$DC = 3AD$,试探究线段$DE$与$CB$之间的数量关系。
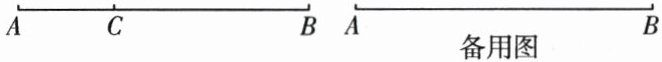
(1)如图,若$BC = 2AC$,$AB = 9$,$D$为$AC$的中点时,求$BE$的长;
(2)若$C$为$BE$的中点,$DC = 3AD$,试探究线段$DE$与$CB$之间的数量关系。
答案:
解:
(1)如图
(1),设AC=x.因为BC=2AC,AB=9,DE=
$\frac{1}{2}$AB,所以BC=2AC=2x,DE=$\frac{9}{2}$,所以x+2x=9,所以x=
3,所以AC=3,BC=6.因为D为AC中点,所以AD=$\frac{1}{2}$AC=
$\frac{3}{2}$,所以BE=AB−AD−DE=9−$\frac{3}{2}$−$\frac{9}{2}$=3,所以BE的长为3.
ADC图
(1)
(2)如图
(2),设DE=a,BC=b.因为C为BE的中点,所以EC=BC=b,所以DC=DE+EC=a+b.因为DC=3AD,所以
AD=$\frac{1}{3}$DC=$\frac{1}{3}$(a+b),所以AB=AD+DC+BC=$\frac{1}{3}$(a+b)
+a+b+b=$\frac{4}{3}$a+$\frac{7}{3}$b.因为DE=$\frac{1}{2}$AB,所以AB=2DE,所以$\frac{4}{3}$a+$\frac{7}{3}$b=2a,所以7b=2a,所以7BC=2DE,所以线段DE与
CB之间的数量关系为7BC=2DE.

解:
(1)如图
(1),设AC=x.因为BC=2AC,AB=9,DE=
$\frac{1}{2}$AB,所以BC=2AC=2x,DE=$\frac{9}{2}$,所以x+2x=9,所以x=
3,所以AC=3,BC=6.因为D为AC中点,所以AD=$\frac{1}{2}$AC=
$\frac{3}{2}$,所以BE=AB−AD−DE=9−$\frac{3}{2}$−$\frac{9}{2}$=3,所以BE的长为3.
ADC图
(1)
(2)如图
(2),设DE=a,BC=b.因为C为BE的中点,所以EC=BC=b,所以DC=DE+EC=a+b.因为DC=3AD,所以
AD=$\frac{1}{3}$DC=$\frac{1}{3}$(a+b),所以AB=AD+DC+BC=$\frac{1}{3}$(a+b)
+a+b+b=$\frac{4}{3}$a+$\frac{7}{3}$b.因为DE=$\frac{1}{2}$AB,所以AB=2DE,所以$\frac{4}{3}$a+$\frac{7}{3}$b=2a,所以7b=2a,所以7BC=2DE,所以线段DE与
CB之间的数量关系为7BC=2DE.

22. (10 分)已知$O$是直线$AB$上一点,$∠COD$是直角,$OE$平分$∠BOC$。
(1)如图(1),
①若$∠AOC = 30^{\circ}$,则$∠DOE$的度数为
②若$∠AOC = \alpha$,求$∠DOE$的度数。
(2)如图(2)的位置关系,探究$∠AOC$与$∠DOE$之间的数量关系,直接写出你的结论。
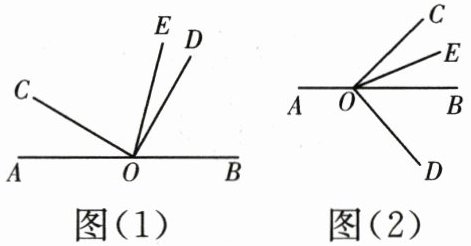
(1)如图(1),
①若$∠AOC = 30^{\circ}$,则$∠DOE$的度数为
15°
;②若$∠AOC = \alpha$,求$∠DOE$的度数。
(2)如图(2)的位置关系,探究$∠AOC$与$∠DOE$之间的数量关系,直接写出你的结论。

答案:
解:
(1)①因为∠AOC=30°,∠AOC+∠BOC=180°,所以∠BOC=180°一∠AOC=150°.因为OE平分∠BOC,所以
∠COE=$\frac{1}{2}$∠BOC=75°.因为∠COD是直角,所以∠COD=
90°=∠DOE+∠COE,所以∠DOE=90°−∠COE=90°−75°=15°.故答案为15°.
②因为∠AOC=α,∠AOC+∠BOC=180°,所以∠BOC=180°一∠AOC=180°一α.因为OE平分∠BOC,所以∠COE=
$\frac{1}{2}$∠BOC=90°−$\frac{1}{2}$α.
因为∠COD是直角,所以∠COD=90°=∠DOE+∠COE,所以∠DOE=90°−∠COE=90°−(90°−$\frac{1}{2}$α)=$\frac{1}{2}$α.
(2)∠AOC=2∠DOE.理由如下:
因为∠COD是直角,OE平分∠BOC,
所以∠COD=∠COE+∠DOE=90°,∠COE=∠BOE,
所以2∠COE+2∠DOE=180°,
因为∠AOC+∠COE+∠BOE=2∠COE+∠AOC=180°,所以∠AOC=2∠DOE.
(1)①因为∠AOC=30°,∠AOC+∠BOC=180°,所以∠BOC=180°一∠AOC=150°.因为OE平分∠BOC,所以
∠COE=$\frac{1}{2}$∠BOC=75°.因为∠COD是直角,所以∠COD=
90°=∠DOE+∠COE,所以∠DOE=90°−∠COE=90°−75°=15°.故答案为15°.
②因为∠AOC=α,∠AOC+∠BOC=180°,所以∠BOC=180°一∠AOC=180°一α.因为OE平分∠BOC,所以∠COE=
$\frac{1}{2}$∠BOC=90°−$\frac{1}{2}$α.
因为∠COD是直角,所以∠COD=90°=∠DOE+∠COE,所以∠DOE=90°−∠COE=90°−(90°−$\frac{1}{2}$α)=$\frac{1}{2}$α.
(2)∠AOC=2∠DOE.理由如下:
因为∠COD是直角,OE平分∠BOC,
所以∠COD=∠COE+∠DOE=90°,∠COE=∠BOE,
所以2∠COE+2∠DOE=180°,
因为∠AOC+∠COE+∠BOE=2∠COE+∠AOC=180°,所以∠AOC=2∠DOE.
查看更多完整答案,请扫码查看


