《2025年核心素养学练评七年级数学上册人教版》

19. (8 分)如图(1),约定：上方相邻两数之和等于这两数下方箭头共同指向的数.示例如图(2),即$4 + 3 = 7$.
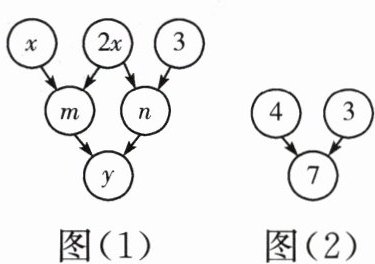
(1)$m = $3x,$n = $______2x+3,$y = $______5x+3；(用含$x$的代数式来表示)
(2)当$x = -2$时,计算$y$的值；
(3)请任写出一个$x$的值,使$y大于10$.

答案： 解:
(1)m=x+2x=3x,n=2x+3,y=m+n=3x+2x+3=5x+3.故答案为3x;2x+3;5x+3.
(2)当x=-2时,y=5x+3=5×(-2)+3=-7.
(3)x=2(答案不唯一).

20. (8 分)(规律探究)用同样大小的两种不同颜色的正方形纸片,按如图方式拼成长方形；
第①个图形中有$2$张正方形纸片；
第②个图形中有$2(1 + 2) = 6 = 2× 3$张正方形纸片；
第③个图形中有$2(1 + 2 + 3) = 12 = 3× 4$张正方形纸片；
第④个图形中有$2(1 + 2 + 3 + 4) = 20 = 4× 5$张正方形纸片；
…

请你观察上述图形与算式,完成下列问题：
(1)第⑤个图形中有______张正方形纸片(直接写出结果)；
(2)根据上面的发现,我们可以猜想第$n$个图形中有______张正方形纸片；
(3)由(1)可得$1 + 2 + 3 + … + n = $______(用含$n$的代数式表示)；
(4)根据你的发现计算：$121 + 122 + 123 + … + 300$.
(1)第⑤个图形中有30张正方形纸片(直接写出结果)；
(2)根据上面的发现,我们可以猜想第$n$个图形中有n(n+1)张正方形纸片；
(3)由(1)可得$1 + 2 + 3 + … + n = $n(n+1)/2(用含$n$的代数式表示)；
(4)根据你的发现计算：$121 + 122 + 123 + … + 300$.
找项数:式子121+122+123+…+300中共有180项.121+122+123+…+300=(120+1)+(120+2)+(120+3)+…+(120+180)=120×180+(1+2+3+…+180)=120×180+180×(180+1)/2=21600+16290=37890.

答案： 解:
(1)因为第①个图形中有2=1×2张正方形纸片;第②个图形中有2(1+2)=6=2×3张正方形纸片;第③个图形中有2(1+2+3)=12=3×4张正方形纸片;第④个图形中有2(1+2+3+4)=20=4×5张正方形纸片,所以第⑤个图形中有5×6=30(张)正方形纸片.故答案为30.
(2)n(n+1).
(3)由
(1)可得1+2+3+…+n=n(n+1)/2.故答案为n(n+1)/2.
(4)找项数:式子121+122+123+…+300中共有180项.121+122+123+…+300=(120+1)+(120+2)+(120+3)+…+(120+180)=120×180+(1+2+3+…+180)=120×180+180×(180+1)/2=21600+16290=37890.