第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
6. 已知在某个时刻时钟的时针与分针所成的最小的角为直角,则这个时刻可能是(
A.$3:30$
B.$9:00$
C.$12:15$
D.$6:45$
B
)A.$3:30$
B.$9:00$
C.$12:15$
D.$6:45$
答案:
B
7. 有两根木棒,一根长 18 cm,另一根长 22 cm,将它们的一端重合且放在同一条直线上,此时两根木棒的中点之间的距离为(
A.2 cm
B.4 cm
C.2 cm 或 22 cm
D.2 cm 或 20 cm
D
)A.2 cm
B.4 cm
C.2 cm 或 22 cm
D.2 cm 或 20 cm
答案:
D
8. 如图,将两个三角尺的直角$∠AOB$与$∠COD$的顶点$O$重合在一起,若$∠AOD = 4∠BOC$,$OE$为$∠BOC$的平分线,则$∠DOE$的度数为(

A.$36^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$72^{\circ}$
D
)
A.$36^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$72^{\circ}$
答案:
D 解析:因为∠AOC+∠BOC=∠AOB=90°,
∠BOD+∠BOC=∠COD=90°,
所以∠AOC+∠BOC+∠BOD+∠BOC=180°,
即∠AOD+∠BOC=180°,
又因为∠AOD=4∠BOC,
所以∠BOC=180°×$\frac{1}{5}$=36°,
因为OE平分∠BOC,
所以∠BOE=∠COE=$\frac{1}{2}$∠BOC=18°,
所以∠DOE=∠COD−∠COE
=90°−18°
=72°.
故选D.
∠BOD+∠BOC=∠COD=90°,
所以∠AOC+∠BOC+∠BOD+∠BOC=180°,
即∠AOD+∠BOC=180°,
又因为∠AOD=4∠BOC,
所以∠BOC=180°×$\frac{1}{5}$=36°,
因为OE平分∠BOC,
所以∠BOE=∠COE=$\frac{1}{2}$∠BOC=18°,
所以∠DOE=∠COD−∠COE
=90°−18°
=72°.
故选D.
9. 如图,$∠1 = ∠2$,$∠3 = ∠4$,$∠AOF = \dfrac{1}{2}∠AOB = 90^{\circ}$,下列说法中正确的是(
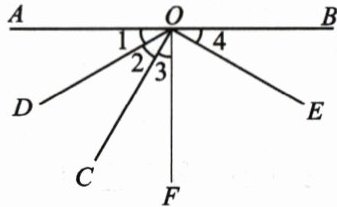
A.射线$OC$是$∠DOF$的平分线
B.$∠4$是$∠AOC$的余角
C.$∠2$的余角是$∠EOF$
D.$∠3$的补角是$∠BOD$
B
)
A.射线$OC$是$∠DOF$的平分线
B.$∠4$是$∠AOC$的余角
C.$∠2$的余角是$∠EOF$
D.$∠3$的补角是$∠BOD$
答案:
B 解析:因为∠AOF=$\frac{1}{2}$∠AOB=90°,
所以∠AOC+∠3=90°.
因为∠3=∠4,所以∠AOC+∠4=90°,
所以∠4是∠AOC的余角,故选B.
所以∠AOC+∠3=90°.
因为∠3=∠4,所以∠AOC+∠4=90°,
所以∠4是∠AOC的余角,故选B.
10. 如图,点$O$为线段$AD$外一点,$M$,$C$,$B$,$N$为$AD$上顺次排列的四点,连接$OA$,$OM$,$OC$,$OB$,$ON$,$OD$,下列结论:①以$O$为顶点的角有 15 个;②若$OM$平分$∠AOC$,$ON$平分$∠BOD$,$∠AOD = 4∠COB$,则$∠MON = \dfrac{3}{2}(∠MOC + ∠BON)$;③若$M$为$AB$的中点,$N$为$CD$的中点,则$MN = \dfrac{1}{2}(AD - CB)$;④若$MC = CB$,$MN = ND$,则$CD = 2CN$。其中正确的结论有(

A.1 个
B.2 个
C.3 个
D.4 个
B
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:
B 解析:①因为经过点O的线段共有6条,所以以O为顶点的角共有1+2+3+4+5=15个,故结论①正确;②设∠AOM=α,∠DON=β,∠COB=θ,则∠MOC=∠AOM=α,∠AOC=2α,∠BON=∠DON=β,∠BOD=2β,所以∠AOD=∠AOC+∠COB+∠BOD=2α+θ+2β,因为∠AOD=4∠COB,所以2α+2β+θ=4θ,所以α+β=$\frac{3}{2}$θ,所以∠MON=∠MOC+∠COB+∠BON=α+θ+β=$\frac{5}{2}$θ,$\frac{3}{2}$(∠MOC+∠BON)=
$\frac{3}{2}$(α+β)=$\frac{9}{4}$θ,故结论②不正确;③设MC=a,CB=b,BN=c,则MB=MC+CB=a+b,CN=CB+BN=b+c,MN=MC+
CB+BN=a+b+c,因为M为AB的中点,N为CD的中点,所以AM=MB=a+b,ND=CN=b+c,所以AD=AM+MN+ND=a+b+a+b+c+b+c=2a+3b+2c,所以$\frac{1}{2}$(AD−
CB)=$\frac{1}{2}$(2a+3b+2c−b)=a+b+c,所以MN=$\frac{1}{2}$(AD−
CB),故结论③正确;④设MC=m,BN=n,则CB=MC=m,所以MN=MC+CB+BN=2m+n,CN=CB+BN=m+n,所以2CN=2m+2n,ND=MN=2m+n,所以CD=CB+
BN+ND=m+n+2m+n=3m+2n,所以CD≠2CN,故结论④不正确.综上所述,正确的结论是①③,共2个.故选B.
$\frac{3}{2}$(α+β)=$\frac{9}{4}$θ,故结论②不正确;③设MC=a,CB=b,BN=c,则MB=MC+CB=a+b,CN=CB+BN=b+c,MN=MC+
CB+BN=a+b+c,因为M为AB的中点,N为CD的中点,所以AM=MB=a+b,ND=CN=b+c,所以AD=AM+MN+ND=a+b+a+b+c+b+c=2a+3b+2c,所以$\frac{1}{2}$(AD−
CB)=$\frac{1}{2}$(2a+3b+2c−b)=a+b+c,所以MN=$\frac{1}{2}$(AD−
CB),故结论③正确;④设MC=m,BN=n,则CB=MC=m,所以MN=MC+CB+BN=2m+n,CN=CB+BN=m+n,所以2CN=2m+2n,ND=MN=2m+n,所以CD=CB+
BN+ND=m+n+2m+n=3m+2n,所以CD≠2CN,故结论④不正确.综上所述,正确的结论是①③,共2个.故选B.
11. 已知$∠1 = 50^{\circ}$,$∠1$与$∠2$互余,则$∠2$的补角的度数为
140°
。
答案:
140° 解析:因为∠1=50°,∠1与∠2互余,
所以∠2=90°−∠1=40°,
所以∠2的补角=180°−∠2=140°.
所以∠2=90°−∠1=40°,
所以∠2的补角=180°−∠2=140°.
12. 如图所示的是一个正方体的表面展开图,且相对面上的两个数之和为 6,则$x - y =$

2
。
答案:
2
查看更多完整答案,请扫码查看


