第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
22. (10 分)数学老师布置了一道思考题:“计算$(-\frac{1}{30})÷ (\frac{2}{3}-\frac{1}{10}+\frac{1}{6}-\frac{2}{5})$”. 小明和小红两位同学经过仔细思考,用不同的方法解答了这个问题:
小明的解法:原式$=(-\frac{1}{30})÷ [(\frac{2}{3}+\frac{1}{6})-(\frac{1}{10}+\frac{2}{5})]$
$=(-\frac{1}{30})÷ (\frac{5}{6}-\frac{1}{2})$
$=-\frac{1}{30}× 3$
$=-\frac{1}{10}$.
小红的解法:原式的倒数为
$(\frac{2}{3}-\frac{1}{10}+\frac{1}{6}-\frac{2}{5})÷ (-\frac{1}{30})$
$=(\frac{2}{3}-\frac{1}{10}+\frac{1}{6}-\frac{2}{5})× (-30)$
$=-20+3-5+12$
$=-10$,
故原式$=-\frac{1}{10}$.
(1)你觉得
(2)请你用自己喜欢的方法计算:
$(-\frac{1}{42})÷ (\frac{1}{6}-\frac{3}{14}+\frac{2}{3}-\frac{2}{7})$.
小明的解法:原式$=(-\frac{1}{30})÷ [(\frac{2}{3}+\frac{1}{6})-(\frac{1}{10}+\frac{2}{5})]$
$=(-\frac{1}{30})÷ (\frac{5}{6}-\frac{1}{2})$
$=-\frac{1}{30}× 3$
$=-\frac{1}{10}$.
小红的解法:原式的倒数为
$(\frac{2}{3}-\frac{1}{10}+\frac{1}{6}-\frac{2}{5})÷ (-\frac{1}{30})$
$=(\frac{2}{3}-\frac{1}{10}+\frac{1}{6}-\frac{2}{5})× (-30)$
$=-20+3-5+12$
$=-10$,
故原式$=-\frac{1}{10}$.
(1)你觉得
小红
的解法更好;(2)请你用自己喜欢的方法计算:
$(-\frac{1}{42})÷ (\frac{1}{6}-\frac{3}{14}+\frac{2}{3}-\frac{2}{7})$.
答案:
(1)小红
(2)原式的倒数为
$(\frac{1}{6}-\frac{3}{14}+\frac{2}{3}-\frac{2}{7})÷(-\frac{1}{42})$
$=(\frac{1}{6}-\frac{3}{14}+\frac{2}{3}-\frac{2}{7})×(-42)$
$=-7+9-28+12$
$=-14$,
故原式$=-\frac{1}{14}$.
(1)小红
(2)原式的倒数为
$(\frac{1}{6}-\frac{3}{14}+\frac{2}{3}-\frac{2}{7})÷(-\frac{1}{42})$
$=(\frac{1}{6}-\frac{3}{14}+\frac{2}{3}-\frac{2}{7})×(-42)$
$=-7+9-28+12$
$=-14$,
故原式$=-\frac{1}{14}$.
23. (11 分)$a,b分别是数轴上两个不同点A,B$所表示的有理数,且$|a|= 5$,$|b|= 2$,$A,B$两点在数轴上的位置如图所示:
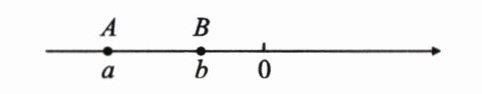
(1)$A,B$两点相距多少个单位长度?
(2)若点$C$在数轴上,点$C到点B的距离是点C到点A距离的\frac{1}{3}$,求点$C$表示的数;
(3)若点$P从点A$出发,沿数轴先向左移动 1 个单位长度,再向右移动 2 个单位长度,再向左移动 3 个单位长度,再向右移动 4 个单位长度…$$依次操作 2025 次后,求点$P$表示的数.
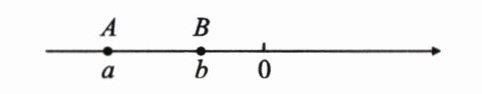
(1)$A,B$两点相距多少个单位长度?
(2)若点$C$在数轴上,点$C到点B的距离是点C到点A距离的\frac{1}{3}$,求点$C$表示的数;
(3)若点$P从点A$出发,沿数轴先向左移动 1 个单位长度,再向右移动 2 个单位长度,再向左移动 3 个单位长度,再向右移动 4 个单位长度…$$依次操作 2025 次后,求点$P$表示的数.
答案:
解:
(1)因为$|a|=5$,$|b|=2$,所以$a=5$或$-5$,$b=2$或$-2$.
由数轴可知$a\lt b\lt0$,所以$a=-5$,$b=-2$.
$-2-(-5)=3$.
答:A,B两点相距3个单位长度.
(2)①若点C在点B的右侧,则$CB=\frac{1}{3}CA=\frac{1}{3}(CB+AB)$,
所以$CB=\frac{1}{2}AB=\frac{3}{2}$.所以点C表示的数为$-2+\frac{3}{2}=-\frac{1}{2}$;
②若点C在A,B两点之间,则$CB=\frac{1}{3}CA=\frac{1}{3}(AB-CB)$,
所以$CB=\frac{1}{4}AB=\frac{3}{4}$.所以点C表示的数为$-2-\frac{3}{4}=-\frac{11}{4}$;
③若点C在点A的左侧,因为$CB\gt CA$,所以不符合题意.
综上所述,点C表示的数为$-\frac{1}{2}$或$-\frac{11}{4}$.
(3)移动2024次后,P点表示的数为$-5-1+2-3+4-5+6-7+\cdots-2023+2024=-5+1+1+1+1+\cdots+1=-5+1×1012=1007$.
移动第2025次后,P点表示的数为
$1007-2025=-1018$.
答:点P表示的数为$-1018$.
(1)因为$|a|=5$,$|b|=2$,所以$a=5$或$-5$,$b=2$或$-2$.
由数轴可知$a\lt b\lt0$,所以$a=-5$,$b=-2$.
$-2-(-5)=3$.
答:A,B两点相距3个单位长度.
(2)①若点C在点B的右侧,则$CB=\frac{1}{3}CA=\frac{1}{3}(CB+AB)$,
所以$CB=\frac{1}{2}AB=\frac{3}{2}$.所以点C表示的数为$-2+\frac{3}{2}=-\frac{1}{2}$;
②若点C在A,B两点之间,则$CB=\frac{1}{3}CA=\frac{1}{3}(AB-CB)$,
所以$CB=\frac{1}{4}AB=\frac{3}{4}$.所以点C表示的数为$-2-\frac{3}{4}=-\frac{11}{4}$;
③若点C在点A的左侧,因为$CB\gt CA$,所以不符合题意.
综上所述,点C表示的数为$-\frac{1}{2}$或$-\frac{11}{4}$.
(3)移动2024次后,P点表示的数为$-5-1+2-3+4-5+6-7+\cdots-2023+2024=-5+1+1+1+1+\cdots+1=-5+1×1012=1007$.
移动第2025次后,P点表示的数为
$1007-2025=-1018$.
答:点P表示的数为$-1018$.
查看更多完整答案,请扫码查看


