《2025年核心素养学练评七年级数学上册人教版》

9. 对于有理数 $a,b$,定义 $a\odot b = 2a - b$,则化简 $[(x + y)\odot(x - y)]\odot3x$ 后可得(C)
A.$-x + y$
B.$-x + 2y$
C.$-x + 6y$
D.$-x + 4y$

答案： C

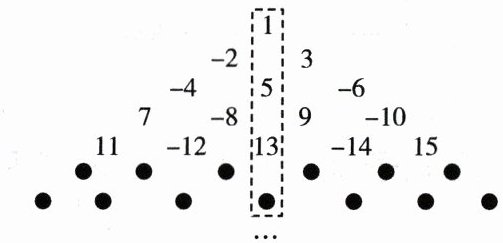
10. 已知一列数：1,$-2$,3,$-4$,5,$-6$,7,…,若将这列数按下图方式排列,则中间在虚线框内的一列数中从上往下数是第 9 个数是(D)

A.$-121$
B.121
C.143
D.145

答案： D 解析:因为中间在虚线框内的一列数,从上至下依次为1,5,13,25,…,这些数都为奇数,且第n个数比前一个数大4(n-1),所以第9个数是145.故选D.

11. 某单项式的系数为 $-\frac{1}{3}$,只含字母 $x,y$,且次数是 3,写出一个符合条件的单项式：$-\frac{1}{3}x^{2}y$(或$-\frac{1}{3}xy^{2}$).

答案： $-\frac{1}{3}x^{2}y$(或$-\frac{1}{3}xy^{2}$) 解析:某单项式的系数为$-\frac{1}{3}$,只含字母x,y,且该单项式的次数是3,则符合条件的单项式可以是$-\frac{1}{3}x^{2}y$或$-\frac{1}{3}xy^{2}$.故答案为$-\frac{1}{3}x^{2}y$(或$-\frac{1}{3}xy^{2}$).

12. 若 $a,b$ 互为相反数,则 $3(3a - 2b)-3(2a - 3b)= $0.

答案： 0

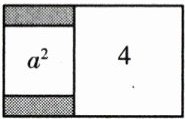
13. 如图,长方形内有两个相邻的正方形,面积分别为 4 和 $a^{2}$,那么阴影部分的面积为$2a-a^{2}$.

答案： $2a-a^{2}$ 解析:因为长方形内有两个相邻的正方形,面积分别为4和$a^{2}$,所以两个正方形的边长分别是2,a,所以阴影部分的面积=2(2+a)-4-$a^{2}$=2a-$a^{2}$.

14.(学科素养 推理能力)已知无论 $x,y$ 取什么值,多项式 $(5x^{2}-my + 10)-(nx^{2}-3y - 1)$ 的值都等于定值 11,则 $m - n$ 的值等于-2.

答案： -2 解析:(5$x^{2}$-my+10)-(n$x^{2}$-3y-1)=5$x^{2}$-my+10-n$x^{2}$+3y+1=(5-n)$x^{2}$+(3-m)y+11,因为无论x,y取什么值,多项式(5$x^{2}$-my+10)-(n$x^{2}$-3y-1)的值都等于定值11,所以5-n=0,3-m=0,所以m=3,n=5,所以m-n=3-5=-2.

15. 如图,用小棒摆下面的图形,图形①需要 3 根小棒,图形②需要 7 根小棒…照这样的规律继续摆下去,图形 $n$ 需要4n-1根小棒.(用含 $n$ 的式子表示)

答案： (4n-1) 解析:图形①有小棒的根数为3=4×1-1;图形②有小棒的根数为7=4×2-1;图形③有小棒的根数为11=4×3-1…图形ⓝ有小棒的根数为4×n-1=4n-1.

16.(6 分)先化简,再求值：
$2(a^{2}b - ab^{2})-3(ab^{2}+a^{2}b - 1)+5ab^{2}-5$,其中有理数 $a,b$ 满足 $|a + 1|+(b - 3)^{2}= 0$.

答案： 解:原式=2$a^{2}$b-2ab$^{2}$-3ab$^{2}$-3$a^{2}$b+3+5ab$^{2}$-5=-$a^{2}$b-2.因为|a+1|+(b-3)$^{2}$=0,所以a+1=0,b-3=0,所以a=-1,b=3,所以原式=-(-1)$^{2}$×3-2=-1×3-2=-5.