第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
例1 “赶陀螺”是一项深受人们喜爱的运动。如图所示是一个陀螺的立体结构图,已知底面圆的直径AB = 8 cm,圆柱体部分的高BC = 6 cm,圆锥体部分的高CD = 3 cm,则这个陀螺的全面积是( )
$A. 68π cm^2$
$B. 74π cm^2$
$C. 84π cm^2$
$D. 100π cm^2$
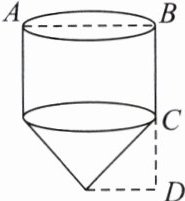
分析:圆锥的表面积加上圆柱的侧面积即为其全面积。
$A. 68π cm^2$
$B. 74π cm^2$
$C. 84π cm^2$
$D. 100π cm^2$

分析:圆锥的表面积加上圆柱的侧面积即为其全面积。
答案:
C
1. 如图,从一张直径是2的圆形纸片上剪出一个圆心角为90°的扇形,若剪出的扇形恰好可以围成一个圆锥,则该圆锥底面圆的面积是( )
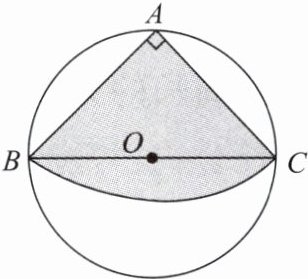
A.π
B.$\frac{π}{4}$
C.$\frac{π}{8}$
D.$\frac{π}{16}$

A.π
B.$\frac{π}{4}$
C.$\frac{π}{8}$
D.$\frac{π}{16}$
答案:
C
2. 如图,已知圆锥的底面半径是4 cm,母线长为12 cm,C为母线PB的中点,求从A到C在圆锥侧面上的最短距离。
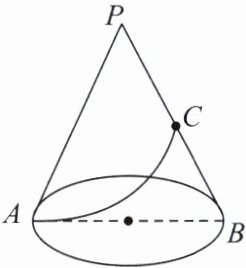
分析:最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为求平面上两点间的距离。先算出圆锥侧面展开图的扇形半径,看如何构成一个直角三角形,然后根据勾股定理进行计算。

分析:最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为求平面上两点间的距离。先算出圆锥侧面展开图的扇形半径,看如何构成一个直角三角形,然后根据勾股定理进行计算。
答案:
$6\sqrt{3}$ cm.
查看更多完整答案,请扫码查看


