第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°,画出旋转后的△AB′C′.
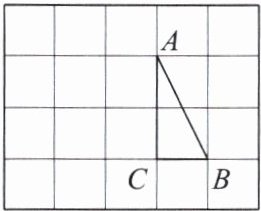

答案:
1. 连接AC、AB。
2. 过点A作AC的垂线,在顺时针方向上截取AC' = AC,确定点C'。
3. 过点A作AB的垂线,在顺时针方向上截取AB' = AB,确定点B'。
4. 连接B'C',△AB'C'即为所求。
(注:因无法直接画图,上述为作图步骤,实际答题时需在方格纸上按步骤画出图形。)
2. 过点A作AC的垂线,在顺时针方向上截取AC' = AC,确定点C'。
3. 过点A作AB的垂线,在顺时针方向上截取AB' = AB,确定点B'。
4. 连接B'C',△AB'C'即为所求。
(注:因无法直接画图,上述为作图步骤,实际答题时需在方格纸上按步骤画出图形。)
例2 如图,在平面直角坐标系中,△OAB的顶点O是坐标原点,AO = AB = 5,OB = 6.
(1)求点A的坐标;
(2)将△AOB绕点B按顺时针方向旋转一定角度后得到△A′O′B,点A的对应点A′在x轴上,求点O的对应点O′的坐标.
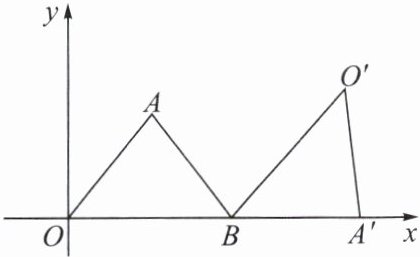
(1)求点A的坐标;
(2)将△AOB绕点B按顺时针方向旋转一定角度后得到△A′O′B,点A的对应点A′在x轴上,求点O的对应点O′的坐标.

答案:
(1)如图,过点A作AC⊥OB于点C,则∠ACO=90°.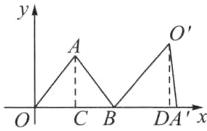
∵AO=AB,AC⊥OB,
∴OC=BC=3. 在Rt△ACO中,∠ACO=90°,
∴AC=√(AO²-OC²)=√(5²-3²)=4,
∴点A的坐标为(3,4).
(2)由旋转的性质可知,△AOB≌△A'O'B',
∴A'B=AB =5,O'B=OB=6. 过点O'作O'D⊥A'B于点D,
∵S△AOB=S△A'O'B',
∴(1/2)·AC·OB=(1/2)·A'B·O'D,
∴(1/2)×4×6=(1/2)×5×O'D,
∴O'D=(24/5).
∵O'D⊥A'B,
∴∠O'DA'=90°. 在Rt△O'BD中,BD=√(O'B²-O'D²)=√(6²-(24/5)²)=18/5,
∴OD=OB+BD=6+(18/5)=48/5,
∴O'(48/5,24/5).
(1)如图,过点A作AC⊥OB于点C,则∠ACO=90°.

∵AO=AB,AC⊥OB,
∴OC=BC=3. 在Rt△ACO中,∠ACO=90°,
∴AC=√(AO²-OC²)=√(5²-3²)=4,
∴点A的坐标为(3,4).
(2)由旋转的性质可知,△AOB≌△A'O'B',
∴A'B=AB =5,O'B=OB=6. 过点O'作O'D⊥A'B于点D,
∵S△AOB=S△A'O'B',
∴(1/2)·AC·OB=(1/2)·A'B·O'D,
∴(1/2)×4×6=(1/2)×5×O'D,
∴O'D=(24/5).
∵O'D⊥A'B,
∴∠O'DA'=90°. 在Rt△O'BD中,BD=√(O'B²-O'D²)=√(6²-(24/5)²)=18/5,
∴OD=OB+BD=6+(18/5)=48/5,
∴O'(48/5,24/5).
2. 如图,Rt△OCB的斜边在y轴上,OC = $\sqrt{3}$,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )
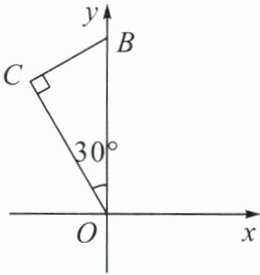
A.($\sqrt{3}$, -1)
B.(1, -$\sqrt{3}$)
C.(2,0)
D.($\sqrt{3}$,0)

A.($\sqrt{3}$, -1)
B.(1, -$\sqrt{3}$)
C.(2,0)
D.($\sqrt{3}$,0)
答案:
A
例3 如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是( )
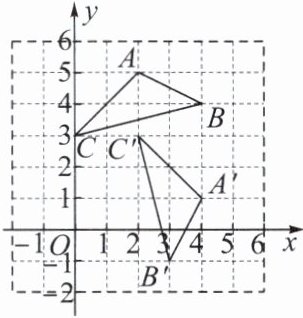
A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)

A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)
答案:
B
3. 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为______.
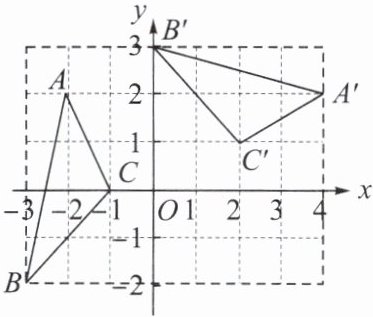

答案:
(1,-1)
查看更多完整答案,请扫码查看


