第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子 $OA$,$O$ 恰为水面中心,安置在柱子顶端 $A$ 处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下. 在过 $OA$ 的任一平面上,建立平面直角坐标系(如图),水流喷出的高度 $y$($m$)与水平距离 $x$($m$)之间的关系式是 $y = -x^2 + 2x + 3$,则下列结论错误的是( )
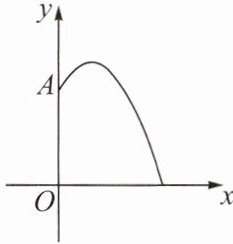
A.柱子 $OA$ 的高度为 $3$ $m$
B.喷出的水流在距柱子 $1$ $m$ 处达到最大高度
C.喷出的水流距水平面的最大高度是 $3$ $m$
D.水池的半径需长于 $3$ $m$ 才能使喷出的水流不至于落在池外

A.柱子 $OA$ 的高度为 $3$ $m$
B.喷出的水流在距柱子 $1$ $m$ 处达到最大高度
C.喷出的水流距水平面的最大高度是 $3$ $m$
D.水池的半径需长于 $3$ $m$ 才能使喷出的水流不至于落在池外
答案:
C
例2 如图,一拱桥的截面呈抛物线形,抛物线两端点与水面的距离都是 $1$ $m$,拱桥的跨度为 $10$ $m$,拱桥与水面的最大距离是 $5$ $m$,桥洞两侧内壁上各有一盏距离水面 $4$ $m$ 的观景灯.
(1) 建立坐标系,求抛物线的解析式;
(2) 求两盏观景灯之间的水平距离.
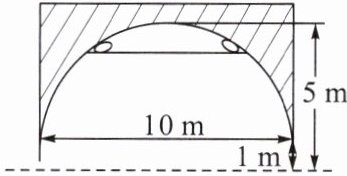
(1) 建立坐标系,求抛物线的解析式;
(2) 求两盏观景灯之间的水平距离.

答案:
(1)建立坐标系略.$y=-\frac{4}{25}x^{2}$. (答案不唯一,由抛物线在坐标系中的位置不同而不同)
(2)$5m$.
(1)建立坐标系略.$y=-\frac{4}{25}x^{2}$. (答案不唯一,由抛物线在坐标系中的位置不同而不同)
(2)$5m$.
查看更多完整答案,请扫码查看


