《2025年四清导航九年级数学上册北师大版辽宁专版》

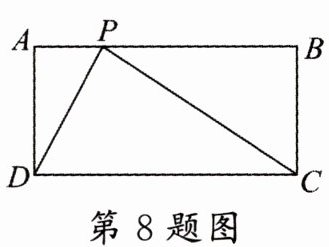
8. (沈阳沈北新区二模)如图,在矩形$ABCD$中,$AB= 10$,$AD= 4$,点$P是边AB$上的一点,若$△ADP与△BCP$相似,则$AP= $2或5或8.

答案： 2或5或8

9. 如图,在$Rt△ABC$中,$∠C= 90^{\circ}$,$AC= 3$,$BC= 4$,点$D$,$E分别是AB$,$AC$边上的动点,将$△ADE沿DE折叠后点A的对应点A'恰好落在BC$边上,当$△A'BD与△ABC$相似时,$AD$的长为$\frac{15}{8}$或$\frac{15}{7}$.

答案： $\frac{15}{8}$或$\frac{15}{7}$

10. 如图,直线$y= \frac{1}{2}x+2与x$轴、$y轴分别交于A$,$B$两点,过该直线上的一点$C(4,m)作CD⊥x轴于点D$,点$E是线段AB$上的一动点,当点$E$的坐标为______时$△OBE与△BCD$相似.

(-2,1)或$(-\frac{8}{5},\frac{6}{5})$

答案： (-2,1)或$(-\frac{8}{5},\frac{6}{5})$

11. 如图,在平面直角坐标系中,已知点$A(1,0)$,点$B(2,0)$,点$C(0,1)$,在坐标轴上有一点$P使得△ACP与△ABC$相似,则点$P$的坐标是(3,0)或(0,2)或(0,3)或(2,0).

答案： (3,0)或(0,2)或(0,3)或(2,0)

12. 如图,在$△ABC$中,$AB= AC= 10\ cm$,$BC= 16\ cm$.点$D由点A出发沿AB方向向点B$匀速运动,同时点$E由点B出发沿BC方向向点C$匀速运动,它们的速度均为$1\ cm/s$.连接$DE$,设运动的时间为$t\ s$($0＜t＜10$).
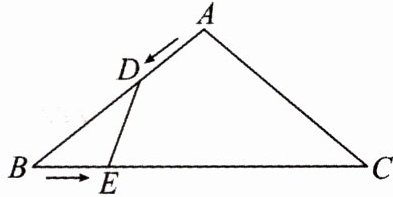
(1)当$t$为何值时,$△BDE的面积为7.5\ cm^2$？
(2)在点$D$,$E$运动的过程中,是否存在$t使得△BDE与△ABC$相似？若存在,请求出$t$的值；若不存在,请说明理由.

答案：
解:根据题意可得BD=(10−t)cm,BE=tcm.
(1)分别过点D，A作DF⊥BC于点F，AG⊥BC于点G，则∠BFD=∠BGA=90°.又
∵∠DBF=∠ABG,
∴△BDF∽△BAG,
∴$\frac{DF}{AG}=\frac{BD}{AB}$.
∵AB=AC=10cm,BC=16cm,
∴BG=$\frac{1}{2}$BC=8cm,
∴AG=$\sqrt{AB^{2}-BG^{2}}=\sqrt{10^{2}-8^{2}}=6$cm,
∴$\frac{DF}{6}=\frac{10−t}{10}$，解得DF=$(6-\frac{3}{5}t)$cm,
∴$S_{\triangle BDE}=\frac{1}{2}BE\cdot DF=\frac{1}{2}t(6-\frac{3}{5}t)=7.5$，整理,得$t^{2}-10t+25=0$，解得$t_{1}=t_{2}=5$，
∴当t的值为5时△BDE的面积为7.5cm²

(2)存在,理由如下:
∵∠B=∠B,
∴分如下2种情况讨论:①当$\frac{BD}{AB}=\frac{BE}{BC}$，即$\frac{10−t}{10}=\frac{t}{16}$时，△DBE∽△ABC，此时解得$t=\frac{80}{13}$；②当$\frac{BE}{AB}=\frac{BD}{BC}$，即$\frac{t}{10}=\frac{10−t}{16}$时，△EBD∽△ABC，此时解得$t=\frac{50}{13}$.综上所述，当$t=\frac{80}{13}$或$\frac{50}{13}$时△BDE与△ABC相似

13. 如图,在平面直角坐标系中,已知点$A(-6,2)$,点$B(-1,-1)$,以点$O$为位似中心,按$1:3的比例把△OAB$缩小,则点$A$的对应点的坐标为$(-2,\frac{2}{3})$或$(2,-\frac{2}{3})$.

答案： $(-2,\frac{2}{3})$或$(2,-\frac{2}{3})$

14. (沈阳东北育才学校一模)如图,在平面直角坐标系中,正方形$ABCD的顶点A的坐标为(1,2)$,边$BC在x$轴上,正方形$EFGH的边FG在x$轴上,且顶点$H的坐标为(9,4)$,则正方形$ABCD与正方形EFGH$的位似中心的坐标为(-3,0)或$(\frac{11}{3},\frac{4}{3})$.

答案： (-3,0)或$(\frac{11}{3},\frac{4}{3})$