第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
8. (铁岭清河区一模)如图,在 $\angle MON$ 的两边上分别截取 $OA$,$OB$,使 $OA = OB$;分别以点 $A$,$B$ 为圆心,以 $OA$ 的长为半径作弧,两弧交于点 $C$;连接 $AC$,$BC$,$AB$,$OC$,若 $AB = 2\ cm$,四边形 $OACB$ 的面积为 $4\ cm^2$,则 $OC$ 的长为(

A.2 cm
B.3 cm
C.4 cm
D.5 cm
C
)
A.2 cm
B.3 cm
C.4 cm
D.5 cm
答案:
C
9. (沈阳沈河区期末)如图,将两张等宽的纸条交叉叠放在一起,在重叠部分构成的四边形 $ABCD$ 中,若 $AB = 10$,$AC = 12$,则 $BD$ 的长为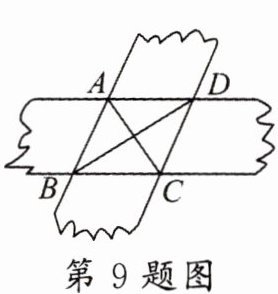
16
.
答案:
16
10. (12 分)(教材 $P9$“随堂练习”$T2$ 变式)如图,在 $\triangle ABC$ 中,$D$,$E$ 分别是 $AB$,$AC$ 的中点,$BE = 2DE$,过点 $C$ 作 $CF // BE$ 交 $DE$ 的延长线于点 $F$.
(1) 求证:四边形 $BCFE$ 是菱形;
(2) 若 $CE = 4$,$\angle BCF = 120°$,求四边形 $BCFE$ 的面积.
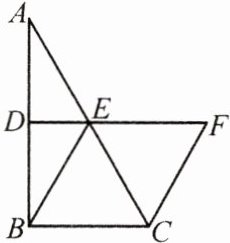
(1) 求证:四边形 $BCFE$ 是菱形;
(2) 若 $CE = 4$,$\angle BCF = 120°$,求四边形 $BCFE$ 的面积.

答案:
解:
(1)证明:
∵D,E分别是AB,AC的中点,
∴DE//BC,BC=2DE.
∵CF//BE,
∴四边形BCFE是平行四边形。
∵BE=2DE,
∴BE=BC,
∴□BCFE是菱形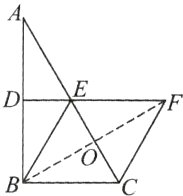
(2)连接BF,交CE于点O.
∵四边形BCFE是菱形,∠BCF=120°,
∴∠CBE=180°−∠BCF=60°,BE=BC,
∴△BCE是等边三角形,
∴BC=CE=2OC=4,
∴OC=2,
∴BF=2BO=2$\sqrt{BC^{2}-OC^{2}}=2\sqrt{4^{2}-2^{2}}=4\sqrt{3}$,
∴S菱形BCFE=$\frac{1}{2}$CE·BF=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$
解:
(1)证明:
∵D,E分别是AB,AC的中点,
∴DE//BC,BC=2DE.
∵CF//BE,
∴四边形BCFE是平行四边形。
∵BE=2DE,
∴BE=BC,
∴□BCFE是菱形

(2)连接BF,交CE于点O.
∵四边形BCFE是菱形,∠BCF=120°,
∴∠CBE=180°−∠BCF=60°,BE=BC,
∴△BCE是等边三角形,
∴BC=CE=2OC=4,
∴OC=2,
∴BF=2BO=2$\sqrt{BC^{2}-OC^{2}}=2\sqrt{4^{2}-2^{2}}=4\sqrt{3}$,
∴S菱形BCFE=$\frac{1}{2}$CE·BF=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$
11. (16 分)(教材 $P9$ 习题 $1.3T3$ 变式)如图,已知 $AE // BF$,$\angle ABF$ 的平分线交 $AE$ 于点 $D$.
(1) 尺规作图:作 $\angle BAE$ 的平分线交 $BF$ 于点 $C$,过点 $A$ 作 $AG \perp BF$ 于点 $G$(尺规作图,保留作图痕迹);
(2) 在 (1) 的条件下,连接 $CD$,
① 求证:四边形 $ABCD$ 是菱形;
② 若 $AC = 16$,$BD = 30$,求 $AG$ 的长.

(1) 尺规作图:作 $\angle BAE$ 的平分线交 $BF$ 于点 $C$,过点 $A$ 作 $AG \perp BF$ 于点 $G$(尺规作图,保留作图痕迹);
(2) 在 (1) 的条件下,连接 $CD$,
① 求证:四边形 $ABCD$ 是菱形;
② 若 $AC = 16$,$BD = 30$,求 $AG$ 的长.

答案:
解:
(1)如图所示: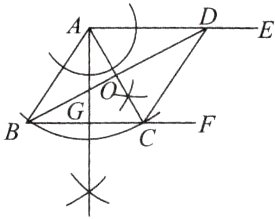
(2)①证明:
∵AE//BF,
∴∠ADB=∠DBC,∠DAC=∠ACB.又
∵AC平分∠BAD,BD平分∠ABC,
∴∠BAC=∠DAC=∠ACB,∠ABD=∠DBC=∠ADB,
∴AB=BC,AB=AD,
∴AD=BC.又
∵AD//BC,
∴四边形ABCD是平行四边形.又
∵AB=AD,
∴□ABCD是菱形
②设AC,BD相交于点O,
∵四边形ABCD是菱形,
∴OA=OC=$\frac{1}{2}$AC=8,OB=OD=$\frac{1}{2}$BD=15,AC⊥BD,
∴AB=$\sqrt{OA^{2}+OB^{2}}=17$.又
∵AG⊥BC,
∴S菱形ABCD=BC·AG=$\frac{1}{2}$AC·BD,即17AG=$\frac{1}{2}$×16×30,解得AG=$\frac{240}{17}$
解:
(1)如图所示:

(2)①证明:
∵AE//BF,
∴∠ADB=∠DBC,∠DAC=∠ACB.又
∵AC平分∠BAD,BD平分∠ABC,
∴∠BAC=∠DAC=∠ACB,∠ABD=∠DBC=∠ADB,
∴AB=BC,AB=AD,
∴AD=BC.又
∵AD//BC,
∴四边形ABCD是平行四边形.又
∵AB=AD,
∴□ABCD是菱形
②设AC,BD相交于点O,
∵四边形ABCD是菱形,
∴OA=OC=$\frac{1}{2}$AC=8,OB=OD=$\frac{1}{2}$BD=15,AC⊥BD,
∴AB=$\sqrt{OA^{2}+OB^{2}}=17$.又
∵AG⊥BC,
∴S菱形ABCD=BC·AG=$\frac{1}{2}$AC·BD,即17AG=$\frac{1}{2}$×16×30,解得AG=$\frac{240}{17}$
微清小贴士 经典 $60°$ 角的菱形-
模型示意图
【已知】如图,点 $E$,$F$ 分别是菱形 $ABCD$ 的边 $BC$,$CD$ 上的点,且 $\angle EAF = \angle B = 60°$.

【结论】$\triangle ABC$ 和 $ \triangle ACD $ 都是
模型示意图
【已知】如图,点 $E$,$F$ 分别是菱形 $ABCD$ 的边 $BC$,$CD$ 上的点,且 $\angle EAF = \angle B = 60°$.

【结论】$\triangle ABC$ 和 $ \triangle ACD $ 都是
等边
三角形 $\Rightarrow \triangle ABE \cong \triangle$ACF
,$\triangle ACE \cong \triangle$ADF
$\Rightarrow \triangle AEF$ 是等边
三角形.
答案:
等边 ACF ADF 等边
1. 如图,点 $E$,$F$ 分别是菱形 $ABCD$ 的边 $BC$,$CD$ 上的点,且 $\angle EAF = \angle D = 60°$,$\angle DAF = 45°$,则 $\angle CFE = $
45°
.
答案:
45°
2. (本溪实验中学第一次月考)如图,在边长为 5 的菱形 $ABCD$ 中,$\angle A = 60°$,点 $E$,$F$ 分别在边 $AD$,$CD$ 上,且 $\angle EBF = 60°$,连接 $EF$,若 $AE = 2$,则 $EF = $

$\sqrt{19}$
.
答案:
$\sqrt{19}$
查看更多完整答案,请扫码查看


