《2025年四清导航九年级数学上册北师大版辽宁专版》

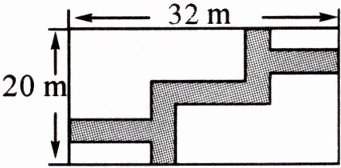
6. (12分)(抚顺新抚区期中)如图,在长为32m,宽为20m的矩形空地上修建同样宽的道路(图中阴影部分),剩余的空地上铺草坪,要使草坪的面积为$540m^2,$求道路的宽.

答案： 解:设道路的宽为x m,根据题意,得$(32-x)$$(20-x)=540$,解得$x_{1}=2$,$x_{2}=50$(不合题意,舍去),$\therefore$道路的宽为2 m

7. (16分)如图,利用一面墙(墙长25m),用总长度为49m的栅栏(图中实线部分)围成一个矩形围栏ABCD,且中间共留两个1m宽的小门,设栅栏BC的长为x m.
(1)若矩形围栏ABCD的面积为$210m^2,$求栅栏BC的长；
(2)矩形围栏ABCD的面积能达到$240m^2$吗?若能,求出相应的x值；若不能,请说明理由.

答案： 解:
(1)根据题意,得$x(49+1+1-3x)=210$,解得$x_{1}=7$,$x_{2}=10$,当$x=7$时,$49+1+1-3x=$$30＞25$,不符合题意,舍去;当$x=10$时,$49+1+$$1-3x=21＜25$,符合题意,$\therefore$栅栏BC的长为10 m
(2)不能,理由如下:当$x(49+1+1-3x)=240$时,整理,得$x^{2}-17x+80=0$,$\because \Delta =(-17)^{2}-$$4× 1× 80=-31＜0$,$\therefore$该方程没有实数根,$\therefore$矩形围栏ABCD的面积不能达到$240\ m^{2}$

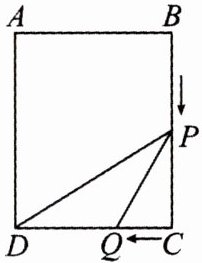
8. (22分)新趋势 动点探究题(铁岭月考改编)如图,在矩形ABCD中,AB= 4cm,BC= 6cm,点P从点B出发沿边BC以2cm/s的速度向C运动,同时点Q从点C出发沿边CD以1cm/s的速度向点D运动,当一个点到达终点时另一点也同时停止.设运动的时间为t s.
(1)填空：CP= (6-2t)cm,DQ= (4-t)cm(用含t的代数式表示),t的取值范围为0≤t≤3；
(2)当t为何值时,PQ的长度为2√5cm？
(3)当t为何值时,△PDQ的面积为$6cm^2？$
(4)是否存在t使得△PDQ为等腰三角形？若存在,请求出t的值；若不存在,请说明理由.

(2)当$PQ=2\sqrt{5}$ cm时,$\because CP^{2}+CQ^{2}=PQ^{2}$,$\therefore (6-2t)^{2}+t^{2}=20$,整理,得$5t^{2}-24t+16=0$,解得$t_{1}=4$(不合题意,舍去),$t_{2}=\frac{4}{5}$,$\therefore$当$t=\frac{4}{5}$时,PQ的长度为$2\sqrt{5}$ cm
(3)当$S_{\triangle PDQ}=\frac{1}{2}DQ\cdot CP=6\ cm^{2}$时,$\frac{1}{2}(4-t)\cdot$$(6-2t)=6$,整理,得$t^{2}-7t+6=0$,解得$t_{1}=1$,$t_{2}=6$(不合题意,舍去),$\therefore$当$t=1$时$\triangle PDQ$的面积为$6\ cm^{2}$
(4)不存在,理由如下:$\because \angle DQP＞90^{\circ}$,$\therefore$要使$\triangle PDQ$为等腰三角形,只需$PQ=DQ$,即$CP^{2}+$$CQ^{2}=PQ^{2}=DQ^{2}$,也即$(6-2t)^{2}+t^{2}=(4-t)^{2}$,整理,得$t^{2}-4t+5=0$,$\because \Delta =(-4)^{2}-4× 1× 5=$$-4＜0$,$\therefore$方程$t^{2}-4t+5=0$无解,$\therefore$不存在t使得$\triangle PDQ$为等腰三角形

答案： 解:
(1)$(6-2t)$ $(4-t)$ $0\leqslant t\leqslant 3$
(2)当$PQ=2\sqrt{5}$ cm时,$\because CP^{2}+CQ^{2}=PQ^{2}$,$\therefore (6-2t)^{2}+t^{2}=20$,整理,得$5t^{2}-24t+16=0$,解得$t_{1}=4$(不合题意,舍去),$t_{2}=\frac{4}{5}$,$\therefore$当$t=\frac{4}{5}$时,PQ的长度为$2\sqrt{5}$ cm
(3)当$S_{\triangle PDQ}=\frac{1}{2}DQ\cdot CP=6\ cm^{2}$时,$\frac{1}{2}(4-t)\cdot$$(6-2t)=6$,整理,得$t^{2}-7t+6=0$,解得$t_{1}=1$,$t_{2}=6$(不合题意,舍去),$\therefore$当$t=1$时$\triangle PDQ$的面积为$6\ cm^{2}$
(4)不存在,理由如下:$\because \angle DQP＞90^{\circ}$,$\therefore$要使$\triangle PDQ$为等腰三角形,只需$PQ=DQ$,即$CP^{2}+$$CQ^{2}=PQ^{2}=DQ^{2}$,也即$(6-2t)^{2}+t^{2}=(4-t)^{2}$,整理,得$t^{2}-4t+5=0$,$\because \Delta =(-4)^{2}-4× 1× 5=$$-4＜0$,$\therefore$方程$t^{2}-4t+5=0$无解,$\therefore$不存在t使得$\triangle PDQ$为等腰三角形