《2025年四清导航九年级数学上册北师大版辽宁专版》

8. 如图,四边形OABC是矩形,点A(2,1),点B(0,5),则点C的坐标是 (D)

A.(-1,3)
B.(-1,2)
C.(-2,3)
D.(-2,4)

答案： D

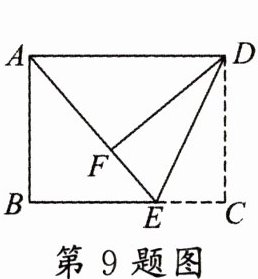
9. (兰州中考)如图,在矩形纸片ABCD中,点E在BC边上,将△CDE沿DE翻折得到△FDE,点F落在AE上. 若CE= 3 cm,AF= 2EF,则AB= 3√5cm.

答案： 3√5

10. (抚顺望花区期中)如图,在矩形ABCD中,AD= 3,CD= 4,点P是AC上的一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF⊥AB于点F,连接EF,则EF的最小值为2.4.

答案： 2.4

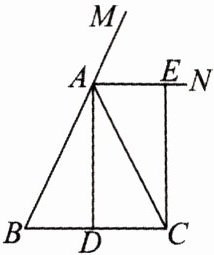
11. (12分)(教材P17例4变式)如图,在△ABC中,AB= AC,D为BC边的中点,过点C作CE//AD,交△ABC的外角∠MAC的平分线AN于点E,求证：四边形ADCE是矩形.

答案： 证明:
∵AB=AC,D为BC的中点，
∴AD⊥BC,∠CAD=1/2∠BAC,
∴∠ADC=90°.又
∵AN平分∠MAC，
∴∠CAE=1/2∠MAC,
∴∠DAE=∠CAD+∠CAE=1/2(∠BAC+∠MAC)=90°.又
∵CE//AD,
∴∠AEC=180° - ∠DAE=90°=∠DAE=∠ADC,
∴四边形ADCE是矩形

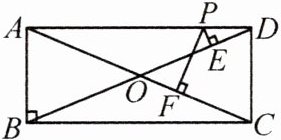
12. (14分)(教材P19习题1.6T5变式)如图,在Rt△ABC中,点O为斜边AC的中点,连接BO并延长到点D,使OD= OB,连接AD,CD.
(1)求证：四边形ABCD为矩形；
(2)P是边AD上的任意一点,过点P分别作PE⊥BD于点E,PF⊥AC于点F,若AD= 12,AB= 5,求PE+PF的值.

答案：
(1)证明:
∵点O为Rt△ABC的斜边AC的中点，
∴∠ABC=90°,OA=OC.又
∵OD=OB,
∴四边形ABCD是平行四边形.又
∵∠ABC=90°,
∴▱ABCD是矩形；
(2)连接OP，
∵AD=12,AB=5,
∴BD=13,S△AOD=1/4S矩形ABCD=1/4×12×5=15,
∴BO=OD=AO=CO=13/2,
∴S△AOD=S△AOP+S△POD=1/2AO·PF+1/2DO·PE=1/2·13/2PF+1/2·13/2PE=15,
∴PE+PF=60/13

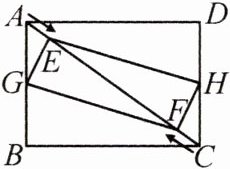
13. (16分)如图,在矩形ABCD中,AB= 3 cm,BC= 4 cm,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1 cm/s,运动时间为t s(0≤t≤5).
(1)填空：AE= tcm,EF= ______|5 - 2t|cm；
(2)若G,H分别是AB,DC的中点,当t为何值时四边形EGFH为矩形？

答案：
(1)t；|5 - 2t|；
(2)
∵四边形ABCD是矩形，
∴AB=CD,AB//CD,
∴∠GAF=∠HCE.又
∵G,H分别是AB,DC的中点，
∴AG=1/2AB=1/2CD=CH.又
∵AE=CF,
∴AF=CE,
∴△AFG≌△CEH(SAS),
∴GF=HE.同理可得△AGE≌△CHF,
∴GE=HF,
∴四边形EGFH是平行四边形.连接GH，易得四边形BCHG是矩形，
∴GH=BC=4cm,
∴当EF=GH,即|5 - 2t|=4时，▱EGFH是矩形,解得t=0.5或t=4.5，
∴当t=0.5或4.5时四边形EGFH为矩形