《2025年四清导航九年级数学上册北师大版辽宁专版》

1. (3 分)下列方程中,是关于 $ x $ 的一元二次方程的是 (D)
A.$\frac{1}{x^{2}} = x^{2} + 2$
B.$ax^{2} + 4x - 5 = 0$($ a $ 为常数)
C.$x(x - 3) = x^{2} + 2$
D.$2x^{2} = 1$

答案： D

2. (6 分)若关于 $ x $ 的方程 $(m - 1)x^{2} + x - 1 = 0$ 是一元二次方程,则 $ m $ 的取值范围是 (A)
A.$m \neq 1$
B.$m = 1$
C.$m \geq 1$
D.$m \neq 0$

答案： A

【变式】若关于 $ x $ 的方程 $4x^{3m - 1} - mx + 1 = 0$ 是一元二次方程,则 $ m $ 的值为1。

答案： 1

3. (9 分)填空：

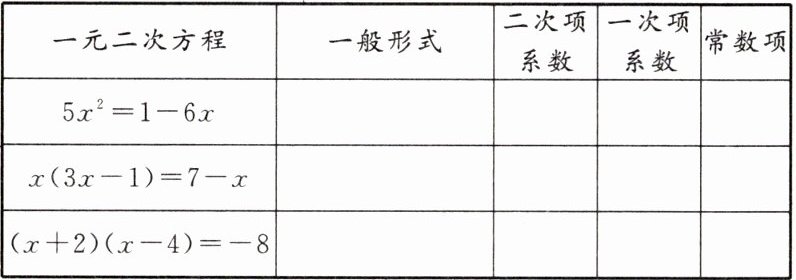
$5x^{2}+6x-1=0$56-1$3x^{2}-7=0$30-7$x^{2}-2x=0$1-20

答案： $5x^{2}+6x-1=0$ 5 6 -1$3x^{2}-7=0$ 3 0 -7$x^{2}-2x=0$ 1 -2 0

4. (3 分)用一根长 $ 40 cm $ 的绳子围成一个面积为 $ 64 cm^{2} $ 的矩形,设该矩形的一边长为 $ x cm $,则可列方程为 (B)
A.$x(20 + x) = 64$
B.$x(20 - x) = 64$
C.$x(40 + x) = 64$
D.$x(40 - x) = 64$

答案： B

5. (4 分)若两个连续奇数的平方和为 $ 244 $,设其中较小的奇数为 $ x $,则可列方程为$x^{2}+(x+2)^{2}=244$。

答案： $x^{2}+(x+2)^{2}=244$

6. (5 分)若关于 $ x $ 的一元二次方程 $2x^{2} - (m + 1)x + 1 = x(x - 1)$ 化成一般形式后二次项的系数为 $ 1 $,一次项的系数为 $ -2 $,则 $ m $ 的值为 (D)
A.$-1$
B.$1$
C.$-2$
D.$2$

答案： D

7. (10 分)【本课时 T2 易错变式】若关于 $ x $ 的方程 $(m + 4)x^{|m| - 2} - 3x = 5$ 是一元二次方程,求 $ m $ 的值。
解：$\because$ 关于 $ x $ 的方程 $(m + 4)x^{|m| - 2} - 3x = 5$ 是一元二次方程,
$\therefore |m| - 2 = 2$,$\therefore |m| = 4$,$\therefore m = \pm 4$。
以上解答正确吗？若不正确,请指出错误的原因,并给出正确的解答过程。

答案： 解:不正确,错解的原因是忽视了"二次项的系数不为0"这一隐含条件,正解的解答过程为:
∵关于x的方程$(m+4)x^{|m|-2}-3x=5$是一元二次方程,$\therefore m+4≠0$且$|m|-2=2,\therefore m=4$

8. (10 分) 新情境 生产生活 请根据题意列出一元二次方程,并将其化成一般形式：
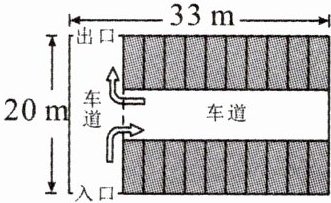
如图是某矩形停车场的平面示意图,其外围的长为 $ 33 m $,宽为 $ 20 m $,其内车道的宽度都相等。若停车位的总占地面积为 $ 510 m^{2} $,求车道的宽度。

答案： 解:设车道的宽度为x m,根据题意可列出一元二次方程$(33-x)(20-x)=510$,将其化成一般形式$x^{2}-53x+150=0$