《2025年四清导航九年级数学上册北师大版辽宁专版》

1. 已知$□ ABCD的对角线AC$,$BD相交于点O$,则下列说法正确的是(D)
A.当$OA = OC$时,$□ ABCD$为矩形
B.当$AB = AD$时,$□ ABCD$为正方形
C.当$\angle ABC = 90^{\circ}$时,$□ ABCD$为菱形
D.当$AC\perp BD$时,$□ ABCD$为菱形

答案： D

2. 如图,在$□ ABCD$中,$E$,$F是对角线AC$上的两点,且$AE = CF$,分别连接$BE$,$BF$,$DE$,$DF$,则下列结论错误的是(D)

A.四边形$BEDF$是平行四边形
B.若四边形$ABCD$是菱形,则四边形$BEDF$也是菱形
C.若四边形$ABCD$是正方形,则四边形$BEDF$是菱形
D.若四边形$ABCD$是矩形,则四边形$BEDF$也是矩形

答案： D

3. 如图,在菱形$ABCD$中,$\angle B = 60^{\circ}$,点$O$为其对称中心,点$E从点A出发沿边AB向点B$移动,到点$B$停止,连接$EO并延长交边CD于点F$,连接$AF$,$CE$,则四边形$AECF$形状的变化依次为(B)

A.平行四边形→矩形→正方形→菱形
B.平行四边形→矩形→平行四边形→菱形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→平行四边形→菱形

答案： B

4. 我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.
(1) 下列说法正确的有(B)
①任意四边形的中点四边形是平行四边形；
②平行四边形的中点四边形是菱形；
③矩形的中点四边形是菱形；
④菱形的中点四边形是正方形；
⑤正方形的中点四边形是正方形.
A. 2个 B. 3个 C. 4个 D. 5个
(2) 如图,四边形$EFGH是四边形ABCD$的中点四边形,连接$AC$,$BD$,
①当$AC$,$BD$满足条件AC=BD时四边形$EFGH$是菱形；
②当$AC$,$BD$满足条件AC⊥BD时四边形$EFGH$是矩形；
③当$AC$,$BD$满足条件AC=BD 且AC⊥BD时四边形$EFGH$是正方形.

答案：
(1)B
(2)①AC=BD ②AC⊥BD ③AC=BD 且AC⊥BD

5. 矩形$ABCD的对角线AC$,$BD相交于点O$,点$F在矩形ABCD$的边上,连接$OF$.若$\angle ADB = 38^{\circ}$,$\angle BOF = 30^{\circ}$,则$\angle AOF = $46°或106°.

答案： 46°或106°

6. 在菱形$ABCD$中,$AB = 5$,$AE是BC$边上的高,$AE = 4$,则对角线$BD$的长为2√5或4√5.

答案： 2√5或4√5

7. (铁岭昌图县期末)在正方形$ABCD$中,$AB = 6$,点$E在直线AD$上,且$DE= \frac{1}{3}AE$,连接$BE$,线段$BE的垂直平分线交CD边于点F$,则$DF$的长为93/16或21/4.

答案： 93/16或21/4

8. 如图,直线$y = -x + 4与x$轴、$y轴分别交于点A$,$B$,点$C是直线AB$上的一动点,点$D$为平面直角坐标系内的任意一点,若以$O$,$A$,$C$,$D$四点为顶点的四边形是菱形,则点$C$的坐标为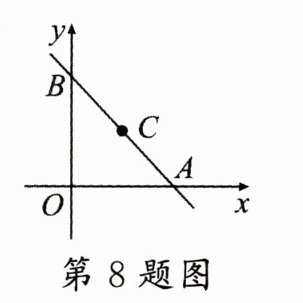(0,4)或(2,2)或(4-2√2,2√2)或(4+2√2,-2√2).

答案： (0,4)或(2,2)或(4-2√2,2√2)或(4+2√2,-2√2)