《2025年四清导航九年级数学上册北师大版辽宁专版》

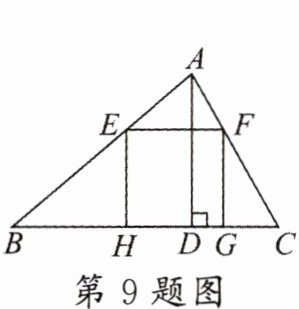
9. (沈阳和平区期末) 如图,在 $ \triangle ABC $ 中,边 $ BC = 60 $,高 $ AD = 40 $,正方形 $ EFGH $ 的顶点 $ E $,$ F $ 分别在边 $ AB $ 和 $ AC $ 上,边 $ GH $ 在 $ BC $ 上,则这个正方形的边长为(C)

A.$ 30 $
B.$ 25 $
C.$ 24 $
D.$ 20 $

答案： C

10. (葫芦岛连山区期末) 图①是装了液体的高脚杯的示意图 (数据如图),用去一部分液体后如图②所示,此时液面 $ AB $ 为(C)

A.$ 1 \, cm $
B.$ 2 \, cm $
C.$ 3 \, cm $
D.$ 4 \, cm $

答案： C

11. 新情境 传统文化 如图,一条河的两岸是平行的,在河的南岸岸边每隔 $ 5 \, m $ 有一棵树,小华站在离南岸 $ 20 \, m $ 的点 $ P $ 处看北岸,在相邻的两棵树之间的空隙中恰好看见一条龙舟的龙头和龙尾 (龙头、龙尾和小华的眼睛位于同一水平平面内),已知龙舟的长为 $ 18.5 \, m $,若龙舟行驶在河的中心,且龙舟与河岸平行,则河的宽度为108 $ m $。

答案： 108

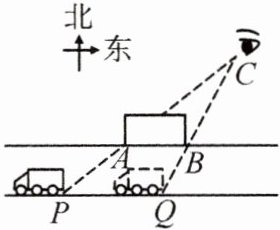
12. (14 分) 新情境 生产生活 某天,小芳走到如图所示的 $ C $ 处时,看到正对面一条东西走向的笔直公路上有一辆汽车从东面驶来,到达 $ Q $ 处时恰好被公路北侧边上竖着的一个长 $ 12 \, m $ 的广告牌 $ AB $ 挡住,$ 3 \, s $ 后在 $ P $ 处又重新看到该汽车的全部车身。已知该汽车的行驶速度是 $ 6 \, m/s $,假设 $ AB // PQ $,公路宽为 $ 10 \, m $,求小芳所在 $ C $ 处到公路南侧 $ PQ $ 的距离。

答案： 解:设小芳所在C处到公路南侧PQ的距离为xm,
∵AB//PQ,
∴易证△CAB∽△CPQ，
∴$\frac{AB}{PQ}=\frac{12}{6×3}=\frac{x-10}{x}$，解得x=30.经检验，x=30是所列方程的解，且符合题意，
∴小芳所在C处到公路南侧PQ的距离为30m

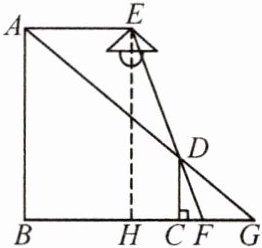
13. (18 分) 新情境 生产生活 小明同学利用数学课所学的知识测量学校门口的路灯的主杆的高度。如图,$ AB $ 为路灯的主杆,$ AE $ 为路灯的悬臂,$ CD $ 是长为 $ 1.8 \, m $ 的标杆。已知路灯的悬臂 $ AE $ 与地面 $ BG $ 平行,当标杆 $ CD $ 竖立于地面时,主杆的顶端 $ A $、标杆的顶端 $ D $ 和地面上的一点 $ G $ 在同一条直线上,此时小明发现路灯的顶端 $ E $、标杆的顶端 $ D $ 和地面上的另一点 $ F $ 也在同一条直线上 (路灯主杆的底端 $ B $、标杆的底端 $ C $ 和地面上的点 $ F $,$ G $ 在同一水平线上),这时小明测得 $ FG $ 的长为 $ 1.5 \, m $,路灯正下方的点 $ H $ 到路灯主杆的底端 $ B $ 的距离为 $ 3 \, m $,求路灯的主杆 $ AB $ 的高度。

答案： 解:延长AE,CD交于点N，
∵AE//BG,AB⊥BG,EH⊥BG,CD⊥BG,
∴AB=EH=CN,AB//EH,AB⊥AN,CN⊥AN,∠EAD=∠G,
∴AE=BH=3m.又
∵∠ADE=∠GDF,
∴△ADE∽△GDF,
∴$\frac{DN}{CD}=\frac{AE}{FG}=\frac{3}{1.5}=2$，
∴DN=2CD=2×1.8=3.6(m),
∴AB=CN=CD+DN=1.8+3.6=5.4(m),
∴路灯的主杆AB 的高度为5.4m