第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
8. 如图,在 $\triangle ABC$ 中,$AB = 6$,$BC = 8$,点 $D$,$E$ 分别是 $AB$,$AC$ 的中点,点 $F$ 在 $DE$ 上,且 $∠AFB = 90^{\circ}$,则 $EF = $
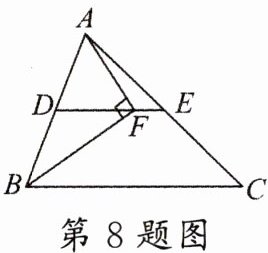
1
。
答案:
1
9. 如图,在正方形 $ABCD$ 中,以对角线 $AC$ 为一边作菱形 $AEFC$,则 $∠FAB$ 的度数为 (
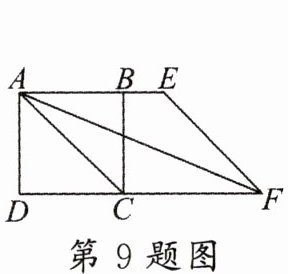
A.$22.5^{\circ}$
B.$28.5^{\circ}$
C.$30^{\circ}$
D.$35.5^{\circ}$
A
)
A.$22.5^{\circ}$
B.$28.5^{\circ}$
C.$30^{\circ}$
D.$35.5^{\circ}$
答案:
A
10. 如图,正方形 $OABC$ 的边 $OA$,$OC$ 分别在 $x$ 轴、$y$ 轴上,等边 $\triangle CDE$ 的顶点 $D$,$E$ 分别在 $OA$,$AB$ 上,连接 $AC$ 交 $DE$ 于点 $F$,若 $AD = 4$,则点 $F$ 的坐标为
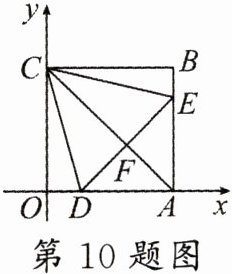
(2$\sqrt{3}$,2)
。
答案:
(2$\sqrt{3}$,2)
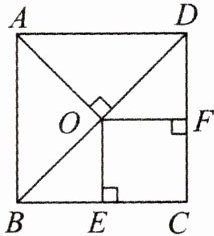
11. 如图,在正方形 $ABCD$ 中,$BD$ 是对角线,$AO⊥BD$ 于点 $O$,$OE⊥BC$ 于点 $E$,$OF⊥CD$ 于点 $F$。
(1)求证:四边形 $OECF$ 是正方形;
(2)若 $AD = 4$,求正方形 $OECF$ 的面积。
(1)求证:四边形 $OECF$ 是正方形;
(2)若 $AD = 4$,求正方形 $OECF$ 的面积。

答案:
解:
(1)证明:
∵四边形ABCD是正方形,
∴AB=AD,∠C=90°,∠OBC=∠ODC=45°.又
∵AO⊥BD,
∴OB=OD.又
∵OE⊥BC,OF⊥DC,
∴∠OEB=∠OEC=∠OFC=∠OFD=90°,
∴四边形OECF是矩形,△OBE≌△ODF (AAS),
∴OE=OF,
∴矩形OECF是正方形
(2)
∵四边形ABCD是正方形,
∴CD=AD=4,∠ODF=45°,
∴∠DOF=90° - ∠ODF=45°=∠ODF,
∴DF=OF.又
∵四边形OECF是正方形,
∴OF=CF,
∴CF=DF=$\frac{1}{2}$CD=2,
∴$S_{正方形OECF}$=CF²=4
(1)证明:
∵四边形ABCD是正方形,
∴AB=AD,∠C=90°,∠OBC=∠ODC=45°.又
∵AO⊥BD,
∴OB=OD.又
∵OE⊥BC,OF⊥DC,
∴∠OEB=∠OEC=∠OFC=∠OFD=90°,
∴四边形OECF是矩形,△OBE≌△ODF (AAS),
∴OE=OF,
∴矩形OECF是正方形
(2)
∵四边形ABCD是正方形,
∴CD=AD=4,∠ODF=45°,
∴∠DOF=90° - ∠ODF=45°=∠ODF,
∴DF=OF.又
∵四边形OECF是正方形,
∴OF=CF,
∴CF=DF=$\frac{1}{2}$CD=2,
∴$S_{正方形OECF}$=CF²=4
12. (沈阳二模)如图,四边形 $ABCD$ 是正方形,以 $CD$ 为边长向正方形外作等边 $\triangle CDE$,$AC$ 与 $BE$ 相交于点 $F$,则 $∠AFD$ 的度数为 (
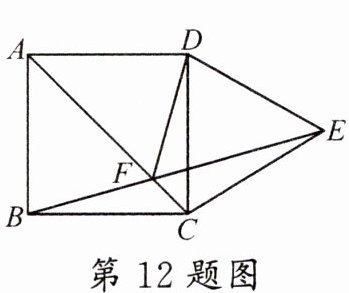
A.$65^{\circ}$
B.$60^{\circ}$
C.$50^{\circ}$
D.$45^{\circ}$
B
)
A.$65^{\circ}$
B.$60^{\circ}$
C.$50^{\circ}$
D.$45^{\circ}$
答案:
B
13. (本溪中考模拟)如图,矩形 $ABCD$ 的边 $AD$ 的长为 $6$,将 $\triangle ACD$ 沿对角线 $AC$ 翻折得到 $\triangle ACD'$,$CD'$ 与 $AB$ 相交于点 $E$,再以 $CD'$ 为折痕将 $\triangle BCE$ 进行翻折得到 $\triangle B'CE$,若两次折叠后点 $B'$ 恰好落在 $\triangle ACD$ 的边上,则 $AB$ 的长为
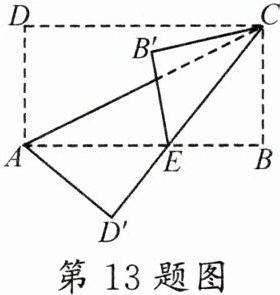
6$\sqrt{3}$或6$\sqrt{2}$+6
。
答案:
6$\sqrt{3}$或6$\sqrt{2}$+6
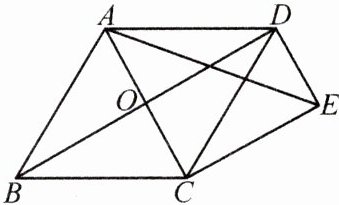
14. (沈阳和平区五模)如图,菱形 $ABCD$ 的对角线 $AC$,$BD$ 相交于点 $O$,过点 $D$ 作 $DE// AC$,且 $DE = \frac{1}{2}AC$,连接 $CE$。
(1)求证:四边形 $OCED$ 是矩形;
(2)连接 $AE$,若菱形 $ABCD$ 的边长为 $8$,$∠ABC = 60^{\circ}$,求 $AE$ 的长。
(1)求证:四边形 $OCED$ 是矩形;
(2)连接 $AE$,若菱形 $ABCD$ 的边长为 $8$,$∠ABC = 60^{\circ}$,求 $AE$ 的长。

答案:
解:
(1)证明:
∵四边形ABCD是菱形,
∴OC=$\frac{1}{2}$AC=DE,AC⊥BD,
∴∠COD=90°.又
∵DE//AC,
∴四边形OCED是平行四边形.又
∵∠COD=90°,
∴▱OCED是矩形
(2)
∵菱形ABCD的边长为8,
∴AB=BC=AD=8.又
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=8,
∴OA=$\frac{1}{2}$AC=4,
∴OD=$\sqrt{AD^2 - OA^2}$=4$\sqrt{3}$.又
∵四边形OCED是矩形,
∴CE=OD=4$\sqrt{3}$,∠OCE=90°,
∴AE=$\sqrt{AC^2 + CE^2}$=4$\sqrt{7}$
(1)证明:
∵四边形ABCD是菱形,
∴OC=$\frac{1}{2}$AC=DE,AC⊥BD,
∴∠COD=90°.又
∵DE//AC,
∴四边形OCED是平行四边形.又
∵∠COD=90°,
∴▱OCED是矩形
(2)
∵菱形ABCD的边长为8,
∴AB=BC=AD=8.又
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=8,
∴OA=$\frac{1}{2}$AC=4,
∴OD=$\sqrt{AD^2 - OA^2}$=4$\sqrt{3}$.又
∵四边形OCED是矩形,
∴CE=OD=4$\sqrt{3}$,∠OCE=90°,
∴AE=$\sqrt{AC^2 + CE^2}$=4$\sqrt{7}$
查看更多完整答案,请扫码查看


