《2025年四清导航九年级数学上册北师大版辽宁专版》

8. (本溪实验中学期末)如图,随机闭合 $4$ 个开关 $S_1, S_2, S_3, S_4$ 中的两个开关,能使小灯泡 $L$ 发光的概率是 (A)

A.$\frac{2}{3}$
B.$\frac{1}{2}$
C.$\frac{1}{3}$
D.$\frac{3}{4}$

答案： A

9. 无色酚酞溶液是一种常用的酸碱指示剂,广泛应用于检验溶液的酸碱性。通常情况下,酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色。现从 $5$ 瓶缺失标签的无色液体：蒸馏水、白醋溶液、食用碱溶液、弱酸性柠檬水溶液、火碱溶液中随机地取出 $2$ 瓶滴入酚酞试剂,则这 $2$ 瓶溶液中只有 $1$ 瓶变红的概率为$\frac{3}{5}$。

答案： $\frac{3}{5}$

10. 如图是某地铁站的进站口,共有 $3$ 个闸机检票通道口,若甲、乙两人各随机选择一个闸机检票通道口进站,则两人从不同的闸机检票通道口进站的概率为$\frac{2}{3}$。

答案： $\frac{2}{3}$

11. 为了迎接“新年购物节”,方便外地游客品尝沈阳鸡架,政府临时创建了鸡架美食广场,里面有最有名的 $A, B, C$ 三家鸡架,小明和小颖每人想随机选一个品尝(选择每种鸡架的机会是相同的),请用画树状图或列表的方法求两人中至少有一人选到 $C$ 家鸡架的概率。

答案：
解:画树状图如下:

由树状图可知共有9种等可能的结果,其中两人中至少有一人选到C家鸡架的结果有5种,$\therefore$两人中至少有一人选到C家鸡架的概率为$\frac{5}{9}$

12. (本溪十二中押题卷)“校园安全”受到全社会的关注,某中学对部分学生就校园安全知识的了解程度采用随机抽样调查的方式进行调查,并根据收集到的信息进行统计后绘制了下面两幅尚不完整的统计图：
请你根据统计图中的信息解答下列问题：
(1) 接受问卷调查的学生共有______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为______°；
(2) 请补全条形统计图；
(3) 若该中学共有学生 $900$ 人,请根据上述调查结果估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；
(4) 若从对校园安全知识达到“了解”程度的 $3$ 个女生和 $2$ 个男生中随机抽取 $2$ 人参加校园安全知识竞赛,请用画树状图或列表的方法求出恰好抽到 $1$ 个男生和 $1$ 个女生的概率。

答案：
解:
(1)60　90
(2)“了解”这组的人数为$60-15-30-10=5$,补全条形统计图略
(3)估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为$900×\frac{5+15}{60}=300$
(4)列表如下:

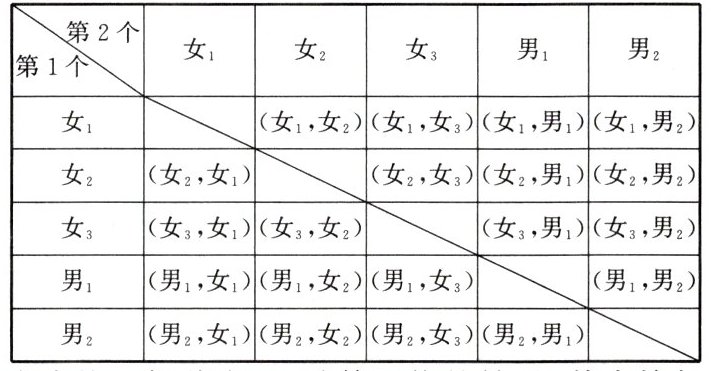
由表格可知共有20种等可能的结果,其中恰好抽到1个男生和1个女生的结果有12种,$\therefore$恰好抽到1个男生和1个女生的概率为$\frac{12}{20}=\frac{3}{5}$