《2025年多维互动提优课堂八年级物理上册提升版》

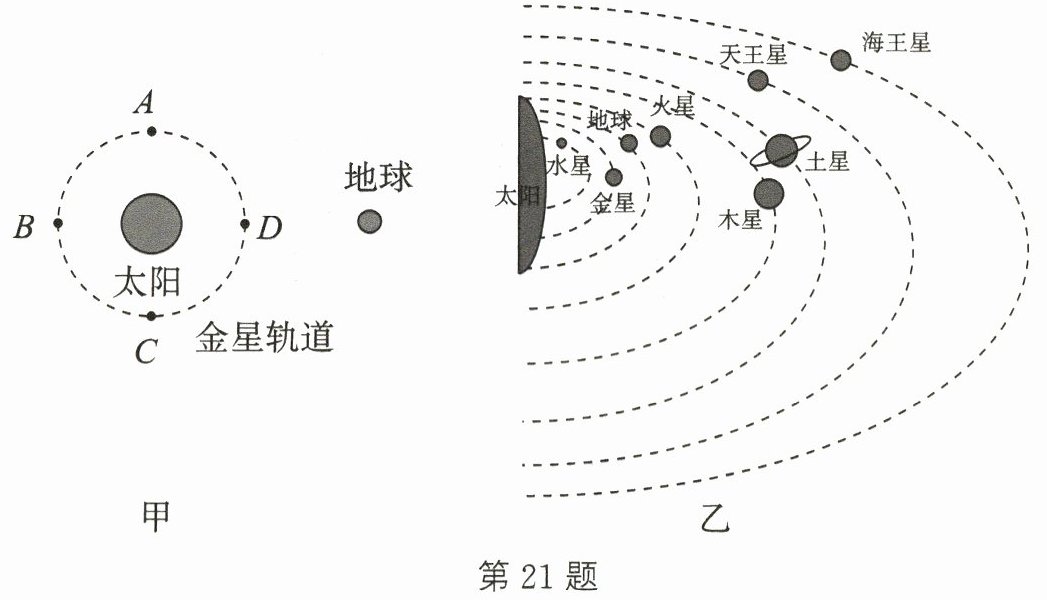
21. 某年6月6日,天空再次上演了“金星凌日”的奇观,即从地球上看去,有一小黑点在太阳表面缓慢移动。
(1)“金星凌日”现象可以用光的直线传播来解释,图甲为发生“金星凌日”现象时的示意图,金星的位置在______D(A/B/C/D)时发生“金星凌日”现象。
(2)图乙为太阳及八大行星示意图。据图分析,你认为在地球上除了可以看到“金星凌日”外,还能看到“水星凌日”现象。

答案： 【解析】：
(1) “金星凌日”现象的成因是光的直线传播。当金星转到太阳与地球中间且三者在一条直线上时，发生“金星凌日”现象，金星的位置在图甲的D处时，在地球上看到金星从太阳面上移过，发生“金星凌日”现象。
(2) 据图分析，在地球和太阳之间还有水星，所以水星有可能转到太阳与地球的中间，且三者在一条直线上时，就会发生“水星凌日”现象。
【答案】：
(1) 光的直线传播；D
(2) 水星

22. 电闪雷鸣时,我们总是先看到闪电后听到雷声,说明光速比声速快(快/慢)。真空中的光速约为$3×10^{8}$m/s。太阳光传播到地球的时间大约为500 s,则太阳到地球的距离大约为$1.5×10^{8}$km。

答案： 【解析】：
这道题目考查的是光速和声速的比较，以及光速在真空中的数值和利用速度公式计算距离。
首先，我们需要知道光速和声速的大小关系，根据常识和物理知识，光速远大于声速。
其次，我们需要记住真空中的光速数值。
最后，利用速度公式$s = vt$（其中$s$是距离，$v$是速度，$t$是时间）来计算太阳到地球的距离。
【答案】：
快；$3 × 10^{8}$；$1.5 × 10^{8}$。
具体计算过程如下：
真空中的光速是$3 × 10^{8} m/s$，所以第二个空填$3 × 10^{8}$。
利用速度公式计算太阳到地球的距离：
$s = vt = 3 × 10^{8} × 500 = 1.5 × 10^{11} m$
由于$1km = 1000m$，所以需要将单位转换为千米：
$1.5 × 10^{11} m = 1.5 × 10^{8} km$
所以第三个空填$1.5 × 10^{8}$。

23. 一束光与水平面成30°角斜射到平静的水面上,则反射角的度数为60°,若入射角增大10°,则入射光线和反射光线夹角的度数为140°。远远望去,一只小鸟在平静的水面上飞翔,若它距水面6 m,它的像距水面的距离是6m,在它向水面俯冲的过程中,像的大小不变(变大/不变/变小)。

答案： 【解析】：
本题主要考查了光的反射定律和平面镜成像的特点。
首先，根据光的反射定律，反射角等于入射角。题目中给出光与水平面成$30^\circ$角斜射到水面上，那么入射角就是$90^\circ-30^\circ=60^\circ$，所以反射角也是$60^\circ$。
其次，若入射角增大$10^\circ$，那么新的入射角就是$70^\circ$，反射角也会增大到$70^\circ$，所以入射光线和反射光线的夹角就是$140^\circ$。
再次，根据平面镜成像的特点，像与物体到平面镜的距离相等。题目中给出小鸟距水面6m，那么它的像距水面的距离也是6m。
最后，平面镜成的像与物体的大小相等，这个大小并不会因为物体与平面镜的距离改变而改变，所以在小鸟向水面俯冲的过程中，像的大小不变。
【答案】：
$60^\circ$；$140^\circ$；6；不变。

24. 如图所示,小明制成了一个针孔照相机,将点燃的蜡烛置于小孔前的适当位置,观察并研究小孔成像的特点。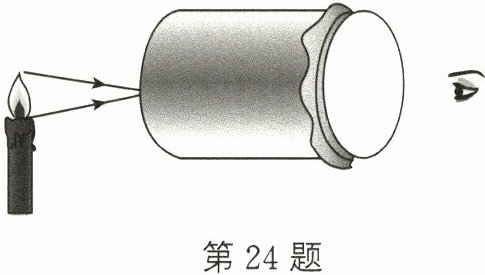
(1)开始实验时,眼睛从光屏一侧看过去,无论怎样调节易拉罐与烛焰之间的距离,用塑料薄膜做的屏上都看不到烛焰的像,只能看到一片光亮,最有可能的原因是小孔太大。
(2)问题解决后,成功在屏上得到烛焰的像,这是倒立(正立/倒立)的实像(实像/虚像)；烛焰在塑料薄膜上所成像的形状与小孔的形状无关(有关/无关)。
(3)小明进一步实验,分别测出烛焰的高度$h_{1}$,烛焰到小孔的距离$x_{1}$,像的高度$h_{2}$,像到小孔的距离$x_{2}$,测多组数据后发现,它们之间满足关系：$\frac{x_{1}}{h_{1}}= \frac{x_{2}}{h_{2}}$；树荫下的圆形光斑就是太阳通过树叶中间的小孔在地面上成的像,小明从网上查到太阳到地面的距离约为$1.5×10^{11}m$,太阳的直径约为$1.4×10^{9}m$,则一个直径为3.5 cm的光斑到它对应的小孔间距约为3.75m。树荫下圆形光斑大小不一的主要原因是小孔到地面的距离不同。

答案：
(1)小孔太大
(2)倒立；实像；无关
(3)解：由题意知，太阳直径$h_{1}=1.4×10^{9}m$，太阳到小孔距离$x_{1}=1.5×10^{11}m$，光斑直径$h_{2}=3.5cm=0.035m$，设光斑到小孔距离为$x_{2}$。
因为$\frac{x_{1}}{h_{1}}=\frac{x_{2}}{h_{2}}$，所以$x_{2}=\frac{x_{1}h_{2}}{h_{1}}=\frac{1.5×10^{11}m×0.035m}{1.4×10^{9}m}=3.75m$
小孔到地面的距离不同