第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
22. 百米赛跑时,某同学前40 m做加速运动,后60 m做匀速运动,通过终点时的速度为6 m/s,测验成绩是15 s。他经过中点(50 m)时的速度是
6
m/s,前40 m的平均速度是8
m/s。
答案:
解:
因后60m做匀速运动,通过终点时的速度为6m/s,故匀速运动阶段速度为6m/s,中点50m处于后60m匀速阶段,所以经过中点时的速度是6m/s。
后60m所用时间:$t_{后}=\frac{s_{后}}{v_{后}}=\frac{60m}{6m/s}=10s$。
前40m所用时间:$t_{前}=t_{总}-t_{后}=15s - 10s=5s$。
前40m的平均速度:$v_{前}=\frac{s_{前}}{t_{前}}=\frac{40m}{5s}=8m/s$。
6;8
因后60m做匀速运动,通过终点时的速度为6m/s,故匀速运动阶段速度为6m/s,中点50m处于后60m匀速阶段,所以经过中点时的速度是6m/s。
后60m所用时间:$t_{后}=\frac{s_{后}}{v_{后}}=\frac{60m}{6m/s}=10s$。
前40m所用时间:$t_{前}=t_{总}-t_{后}=15s - 10s=5s$。
前40m的平均速度:$v_{前}=\frac{s_{前}}{t_{前}}=\frac{40m}{5s}=8m/s$。
6;8
23. (10分)在“比较纸锥下落快慢”的实验中:
(1)如图甲中①所示,两个等大的圆纸片裁去大小不等的扇形,做成如图甲中②所示的A、B两个锥角不等的纸锥。
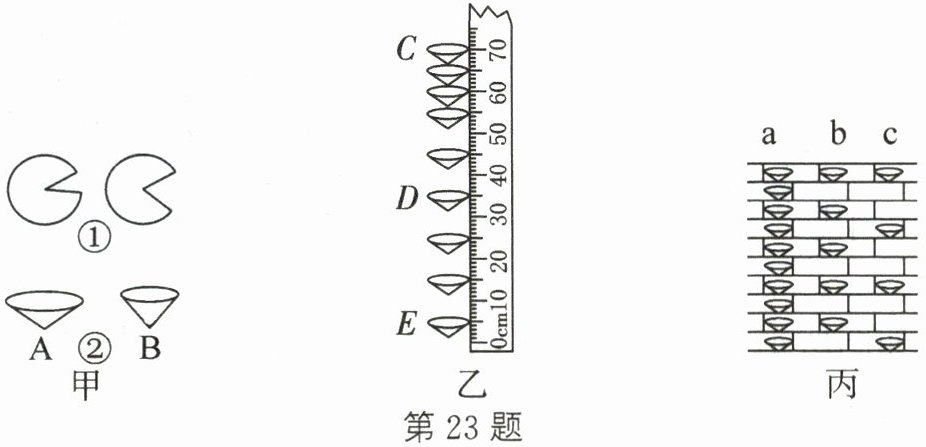
(2)实验要测量的物理量有下落的时间和
(3)为了便于测量下落的时间,应选择图甲②中的纸锥
(4)小芳所在的兴趣小组用频闪照相的方式探究纸锥竖直下落的运动情况,照相机每隔0.2 s曝光一次。兴趣小组拍下的照片如图乙所示,由此可以判断此纸锥从C到E下落的过程中速度的变化情况是
(5)小明使a、b、c三个形状相同但质量不同的纸锥从不同高度落下,用频闪照相的方式通过每隔相等的时间曝光一次的方法记录纸锥的运动过程,如图丙所示是其中一段的示意图。据图可知,这段过程中做匀速直线运动的是
(1)如图甲中①所示,两个等大的圆纸片裁去大小不等的扇形,做成如图甲中②所示的A、B两个锥角不等的纸锥。

(2)实验要测量的物理量有下落的时间和
下落的高度
。(3)为了便于测量下落的时间,应选择图甲②中的纸锥
A
(A/B)进行实验较好。(4)小芳所在的兴趣小组用频闪照相的方式探究纸锥竖直下落的运动情况,照相机每隔0.2 s曝光一次。兴趣小组拍下的照片如图乙所示,由此可以判断此纸锥从C到E下落的过程中速度的变化情况是
先变大后不变
(不变/先变大后不变/一直变大)。D、E两位置间纸锥的平均速度为1
m/s。(5)小明使a、b、c三个形状相同但质量不同的纸锥从不同高度落下,用频闪照相的方式通过每隔相等的时间曝光一次的方法记录纸锥的运动过程,如图丙所示是其中一段的示意图。据图可知,这段过程中做匀速直线运动的是
b
。
答案:
【解析】:
本题主要考查“比较纸锥下落快慢”的实验,涉及实验原理、物理量的测量、实验器材的选择、速度变化的分析以及平均速度的计算等知识点。
(2)实验中需要测量纸锥下落的时间和下落的高度,通过比较下落相同高度所用时间的长短或相同时间内下落高度的多少来比较纸锥下落的快慢。
(3)为了便于测量下落的时间,应选择下落速度较慢的纸锥,锥角越大,下落速度越慢,所以应选择图甲②中的纸锥A进行实验较好。
(4)由图乙可知,纸锥从C到D的过程中,相邻两个纸锥间的距离逐渐增大,说明速度逐渐变大;从D到E的过程中,相邻两个纸锥间的距离相等,说明速度不变。所以此纸锥从C到E下落的过程中速度的变化情况是先变大后不变。D、E两位置间纸锥下落的高度$h = 50.0cm - 10.0cm = 40.0cm = 0.4m$,时间$t = 0.2s×2 = 0.4s$,根据平均速度公式$v=\frac{s}{t}$,可得D、E两位置间纸锥的平均速度$v=\frac{0.4m}{0.4s}=1m/s$。
(5)匀速直线运动是指在相等的时间内通过的路程相等。由图丙可知,在相等的时间内,a纸锥通过的路程越来越大,是加速运动;b纸锥在相等的时间内通过的路程相等,是匀速直线运动;c纸锥在相等的时间内通过的路程越来越小,是减速运动。所以这段过程中做匀速直线运动的是b。
【答案】:
(2)下落的高度
(3)A
(4)先变大后不变;1
(5)b
本题主要考查“比较纸锥下落快慢”的实验,涉及实验原理、物理量的测量、实验器材的选择、速度变化的分析以及平均速度的计算等知识点。
(2)实验中需要测量纸锥下落的时间和下落的高度,通过比较下落相同高度所用时间的长短或相同时间内下落高度的多少来比较纸锥下落的快慢。
(3)为了便于测量下落的时间,应选择下落速度较慢的纸锥,锥角越大,下落速度越慢,所以应选择图甲②中的纸锥A进行实验较好。
(4)由图乙可知,纸锥从C到D的过程中,相邻两个纸锥间的距离逐渐增大,说明速度逐渐变大;从D到E的过程中,相邻两个纸锥间的距离相等,说明速度不变。所以此纸锥从C到E下落的过程中速度的变化情况是先变大后不变。D、E两位置间纸锥下落的高度$h = 50.0cm - 10.0cm = 40.0cm = 0.4m$,时间$t = 0.2s×2 = 0.4s$,根据平均速度公式$v=\frac{s}{t}$,可得D、E两位置间纸锥的平均速度$v=\frac{0.4m}{0.4s}=1m/s$。
(5)匀速直线运动是指在相等的时间内通过的路程相等。由图丙可知,在相等的时间内,a纸锥通过的路程越来越大,是加速运动;b纸锥在相等的时间内通过的路程相等,是匀速直线运动;c纸锥在相等的时间内通过的路程越来越小,是减速运动。所以这段过程中做匀速直线运动的是b。
【答案】:
(2)下落的高度
(3)A
(4)先变大后不变;1
(5)b
24. (8分)甲、乙两地的距离是900 km,一列火车早上7:30从甲地出发开往乙地,途中停靠了几个车站,在当日16:30到达乙地。火车行驶途中以144 km/h的速度匀速通过长度为400 m的桥梁,火车全部通过桥梁的时间是25 s。问:
(1)火车从甲地开往乙地的平均速度是多少?
(2)火车的长度是多少?
(1)火车从甲地开往乙地的平均速度是多少?
(2)火车的长度是多少?
答案:
【解析】:
本题主要考查了平均速度和速度公式的应用,以及如何从题目中提取关键信息。
(1)要求火车从甲地开往乙地的平均速度,需要知道火车行驶的总路程和总时间。总路程题目已给出为$900km$,总时间可以通过火车的出发和到达时间计算得出。然后利用平均速度的定义式$v = \frac{s}{t}$($s$为总路程,$t$为总时间)计算。
(2)要求火车的长度,可以利用火车通过桥梁时的速度和时间来计算。火车通过桥梁的总路程等于桥梁长度加上火车长度,已知火车速度和通过桥梁的时间,可以通过速度公式$s = vt$($s$为路程,$v$为速度,$t$为时间)计算出火车通过桥梁的总路程,再减去桥梁长度即可得到火车长度。
【答案】:
(1)火车从甲地出发时间为早上$7:30$,即$7 × 60 + 30 = 450$(min),到达乙地时间为当日$16:30$,即$16 × 60 + 30 = 990$(min)。
所以火车行驶的总时间为:$t = 990 - 450 = 540$(min),换算成小时为$t = \frac{540}{60} = 9$(h)。
根据平均速度的定义式,火车从甲地开往乙地的平均速度为:$v = \frac{s}{t} = \frac{900}{9} = 100$($km/h$)。
综上:火车从甲地开往乙地的平均速度是$100km/h$。
(2)火车通过桥梁的速度为$v^{\prime} = 144km/h = 40m/s$(因为$1km/h=\frac{1000}{3600} m/s=\frac{5}{18} m/s$,所以$144km/h=144× \frac{5}{18} m/s=40m/s$),通过桥梁的时间为$t^{\prime} = 25s$。
根据速度公式,火车通过桥梁的总路程为:$s^{\prime} = v^{\prime}t^{\prime} = 40 × 25 = 1000$(m)。
由于火车通过桥梁的总路程等于桥梁长度加上火车长度,所以火车的长度为:$L = s^{\prime} - s_{桥} = 1000 - 400 = 600$(m)。
综上:火车的长度是$600m$。
本题主要考查了平均速度和速度公式的应用,以及如何从题目中提取关键信息。
(1)要求火车从甲地开往乙地的平均速度,需要知道火车行驶的总路程和总时间。总路程题目已给出为$900km$,总时间可以通过火车的出发和到达时间计算得出。然后利用平均速度的定义式$v = \frac{s}{t}$($s$为总路程,$t$为总时间)计算。
(2)要求火车的长度,可以利用火车通过桥梁时的速度和时间来计算。火车通过桥梁的总路程等于桥梁长度加上火车长度,已知火车速度和通过桥梁的时间,可以通过速度公式$s = vt$($s$为路程,$v$为速度,$t$为时间)计算出火车通过桥梁的总路程,再减去桥梁长度即可得到火车长度。
【答案】:
(1)火车从甲地出发时间为早上$7:30$,即$7 × 60 + 30 = 450$(min),到达乙地时间为当日$16:30$,即$16 × 60 + 30 = 990$(min)。
所以火车行驶的总时间为:$t = 990 - 450 = 540$(min),换算成小时为$t = \frac{540}{60} = 9$(h)。
根据平均速度的定义式,火车从甲地开往乙地的平均速度为:$v = \frac{s}{t} = \frac{900}{9} = 100$($km/h$)。
综上:火车从甲地开往乙地的平均速度是$100km/h$。
(2)火车通过桥梁的速度为$v^{\prime} = 144km/h = 40m/s$(因为$1km/h=\frac{1000}{3600} m/s=\frac{5}{18} m/s$,所以$144km/h=144× \frac{5}{18} m/s=40m/s$),通过桥梁的时间为$t^{\prime} = 25s$。
根据速度公式,火车通过桥梁的总路程为:$s^{\prime} = v^{\prime}t^{\prime} = 40 × 25 = 1000$(m)。
由于火车通过桥梁的总路程等于桥梁长度加上火车长度,所以火车的长度为:$L = s^{\prime} - s_{桥} = 1000 - 400 = 600$(m)。
综上:火车的长度是$600m$。
查看更多完整答案,请扫码查看


