《2025年假期新思维七年级数学北师大版》

考点1 对顶角、邻补角
考点突破：熟练掌握角平分线定义及性质是解这类题的关键。注意区分对顶角、邻补角。
1. 如图,已知直线$AB与CD交于点O$,$ON平分∠BOD$,若$∠BOC= 110^{\circ }$,求$∠AON$的度数。

答案： 解:
∵直线AB与CD交于点O，∠BOC=110°，
∴∠BOD=180°-∠BOC=180°-110°=70°（邻补角互补），
∠AOD=∠BOC=110°（对顶角相等）。
∵ON平分∠BOD，
∴∠DON=∠BOD÷2=70°÷2=35°（角平分线定义）。
∴∠AON=∠AOD+∠DON=110°+35°=145°。

2. 如图,$AB⊥AC$,$AD⊥BC$,垂足分别为$A、D$,则图中能表示点到直线距离的线段共有 (D)

A.$2$条
B.$3$条
C.$4$条
D.$5$条

答案： 2. D

3. 如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道$ABCD$,使其拐角$∠ABC= 150^{\circ },∠BCD= 30^{\circ }$,则 (C)

A.$AB// BC$
B.$BC// CD$
C.$AB// DC$
D.$AB与CD$相交

答案： 3. C

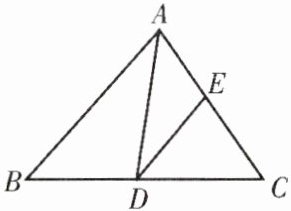
4. 如图,在$△ABC$中,$∠B+∠C= 110^{\circ }$,$AD平分∠BAC$,交$BC于点D$,$DE// AB$,交$AC于点E$,求$∠ADE$等于35度。

答案： 4. 35

5. 如图所示,已知$∠1+∠2= 180^{\circ },∠3= ∠B$,请判断$∠AED与∠C$的大小关系,并证明理由。

答案： 解：∠AED=∠C。理由如下：
∵∠4+∠1=180°（邻补角的定义），∠1+∠2=180°（已知），
∴∠4=∠2（同角的补角相等），
∴EF//AB（内错角相等，两直线平行），
∴∠3=∠ADE（两直线平行，内错角相等）。
又
∵∠3=∠B（已知），
∴∠B=∠ADE（等量代换），
∴DE//BC（同位角相等，两直线平行），
∴∠AED=∠C（两直线平行，同位角相等）。

6. 如图所示,将长方形纸片$ABCD$折叠,使点$D与点B$重合,点$C落在点C'$处,折痕为$EF$,若$∠ABE= 20^{\circ }$,求$∠EFC'$的度数。

答案： 解：在长方形ABCD中，∠A=90°，AD//BC。
∵∠ABE=20°，
∴∠AEB=180°-∠A-∠ABE=180°-90°-20°=70°。
∴∠BED=180°-∠AEB=180°-70°=110°（邻补角定义）。
由折叠性质得∠DEF=∠BEF，∠EFC=∠EFC'。
∵∠DEF+∠BEF=∠BED，
∴∠DEF=∠BED/2=110°/2=55°。
∵AD//BC，
∴∠DEF+∠EFC=180°（两直线平行，同旁内角互补）。
∴∠EFC=180°-∠DEF=180°-55°=125°。
∴∠EFC'=∠EFC=125°。

7. 如图,已知$AB// CD$,直线$AB,CD分别与直线MN相交于点E,F$,$EG平分∠BEN$,$FH平分∠DFN$,试说明$EG// FH$。

答案： 解：因为$AB// CD$，所以$\angle BEN = \angle DFN$。
因为$EG$平分$\angle BEN$，$FH$平分$\angle DFN$，
所以$\angle GEN = \frac{1}{2}\angle BEN$，$\angle HFN = \frac{1}{2}\angle DFN$。
所以$\angle GEN = \angle HFN$。
所以$EG// FH$。