2025年假期新思维七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期新思维七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
22. (9分)新学期开学,两摞规格相同准备发放的数学课本整齐地叠放在讲台上,请根据图中所给的数据信息,解答下列问题.
(1)一本数学课本的高度是多少厘米?
(2)讲台的高度是多少厘米?
(3)请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含用x的代数式表示)
(4)若桌面上有56本同样的数学课本,整齐叠放成一摞,从中取走18本后,求余下的数学课本距离地面的高度.
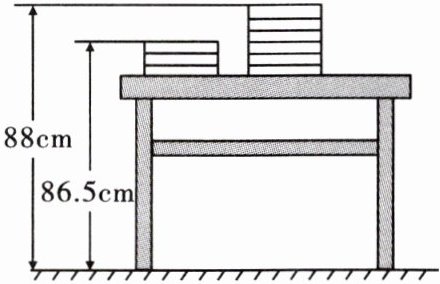
(1)一本数学课本的高度是多少厘米?
(2)讲台的高度是多少厘米?
(3)请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含用x的代数式表示)
(4)若桌面上有56本同样的数学课本,整齐叠放成一摞,从中取走18本后,求余下的数学课本距离地面的高度.

答案:
解:
(1) 由题意可得,
一本数学课本的高度是:$ ( 88 - 86.5 ) ÷ 3 = 1.5 ÷ 3 = 0.5 $ (厘米),
答:一本数学课本的高度是 $ 0.5 $ 厘米;
(2) 讲台的高度是:$ 86.5 - 3 × 0.5 = 86.5 - 1.5 = 85 $ (厘米),
即讲台的高度是 $ 85 $ 厘米;
(3) 整齐叠放在桌面上的 $ x $ 本数学课本距离地面的高度是:$ ( 85 + 0.5 x ) $ 厘米;
(4) 余下的数学课本距离地面的高度:$ 85 + ( 56 - 18 ) × 0.5 = 85 + 38 × 0.5 = 85 + 19 = 104 $ (厘米);
即余下的数学课本距离地面的高度是 $ 104 $ 厘米。
(1) 由题意可得,
一本数学课本的高度是:$ ( 88 - 86.5 ) ÷ 3 = 1.5 ÷ 3 = 0.5 $ (厘米),
答:一本数学课本的高度是 $ 0.5 $ 厘米;
(2) 讲台的高度是:$ 86.5 - 3 × 0.5 = 86.5 - 1.5 = 85 $ (厘米),
即讲台的高度是 $ 85 $ 厘米;
(3) 整齐叠放在桌面上的 $ x $ 本数学课本距离地面的高度是:$ ( 85 + 0.5 x ) $ 厘米;
(4) 余下的数学课本距离地面的高度:$ 85 + ( 56 - 18 ) × 0.5 = 85 + 38 × 0.5 = 85 + 19 = 104 $ (厘米);
即余下的数学课本距离地面的高度是 $ 104 $ 厘米。
23. (内江中考)(12分)观察下列等式:
第一个等式:
$a_{1}= \frac {2}{1+3×2+2×2^{2}}= \frac {1}{2+1}-\frac {1}{2^{2}+1}$
第二个等式:
$a_{2}= \frac {2^{2}}{1+3×2^{2}+2×(2^{2})^{2}}= \frac {1}{2^{2}+1}-\frac {1}{2^{3}+1}$
第三个等式:
$a_{3}= \frac {2^{3}}{1+3×2^{3}+2×(2^{3})^{2}}= \frac {1}{2^{3}+1}-\frac {1}{2^{4}+1}$
第四个等式:
$a_{4}= \frac {2^{4}}{1+3×2^{4}+2×2(2^{4})^{2}}= \frac {1}{2^{4}+1}-\frac {1}{2^{5}+1}$
按上述规律,回答下列问题:
(1)请写出第六个等式:$a_{6}=$
(2)用含n的代数式表示第n个等式:$a_{n}=$
(3)$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+a_{6}=$
(4)计算:$a_{1}+a_{2}+... +a_{n}$.
第一个等式:
$a_{1}= \frac {2}{1+3×2+2×2^{2}}= \frac {1}{2+1}-\frac {1}{2^{2}+1}$
第二个等式:
$a_{2}= \frac {2^{2}}{1+3×2^{2}+2×(2^{2})^{2}}= \frac {1}{2^{2}+1}-\frac {1}{2^{3}+1}$
第三个等式:
$a_{3}= \frac {2^{3}}{1+3×2^{3}+2×(2^{3})^{2}}= \frac {1}{2^{3}+1}-\frac {1}{2^{4}+1}$
第四个等式:
$a_{4}= \frac {2^{4}}{1+3×2^{4}+2×2(2^{4})^{2}}= \frac {1}{2^{4}+1}-\frac {1}{2^{5}+1}$
按上述规律,回答下列问题:
(1)请写出第六个等式:$a_{6}=$
$\frac {2^{6}}{1+3×2^{6}+2×(2^{6})^{2}}$
=$\frac {1}{2^{6}+1}-\frac {1}{2^{7}+1}$
;(2)用含n的代数式表示第n个等式:$a_{n}=$
$\frac {2^{n}}{1+3×2^{n}+2×(2^{n})^{2}}$
=$\frac {1}{2^{n}+1}-\frac {1}{2^{n+1}+1}$
;(3)$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}+a_{6}=$
$\frac {14}{43}$
(得出最简结果);(4)计算:$a_{1}+a_{2}+... +a_{n}$.
$\frac {2^{n+1}-2}{3(2^{n+1}+1)}$
答案:
解:
(1) 由题意知,$ a _ { 6 } = \frac { 2 ^ { 6 } } { 1 + 3 × 2 ^ { 6 } + 2 × ( 2 ^ { 6 } ) ^ { 2 } } = \frac { 1 } { 2 ^ { 6 } + 1 } - \frac { 1 } { 2 ^ { 7 } + 1 } $;
(2) $ a _ { n } = \frac { 2 ^ { n } } { 1 + 3 × 2 ^ { n } + 2 × ( 2 ^ { n } ) ^ { 2 } } = \frac { 1 } { 2 ^ { n } + 1 } - \frac { 1 } { 2 ^ { n + 1 } + 1 } $;
(3) 原式 $ = \frac { 1 } { 2 + 1 } - \frac { 1 } { 2 ^ { 2 } + 1 } + \frac { 1 } { 2 ^ { 2 } + 1 } - \frac { 1 } { 2 ^ { 3 } + 1 } + \frac { 1 } { 2 ^ { 3 } + 1 } - \frac { 1 } { 2 ^ { 4 } + 1 } + \frac { 1 } { 2 ^ { 4 } + 1 } - \frac { 1 } { 2 ^ { 5 } + 1 } + \frac { 1 } { 2 ^ { 5 } + 1 } - $
$ \frac { 1 } { 2 ^ { 6 } + 1 } + \frac { 1 } { 2 ^ { 6 } + 1 } - \frac { 1 } { 2 ^ { 7 } + 1 } = \frac { 1 } { 2 + 1 } - \frac { 1 } { 2 ^ { 7 } + 1 } = \frac { 14 } { 43 } $;
(4) 原式 $ = \frac { 1 } { 2 + 1 } - \frac { 1 } { 2 ^ { 2 } + 1 } + \frac { 1 } { 2 ^ { 2 } + 1 } - \frac { 1 } { 2 ^ { 3 } + 1 } + \cdots + \frac { 1 } { 2 ^ { n } + 1 } - \frac { 1 } { 2 ^ { n + 1 } + 1 } = \frac { 1 } { 2 + 1 } - \frac { 1 } { 2 ^ { n + 1 } + 1 } = $
$ \frac { 2 ^ { n + 1 } - 2 } { 3 ( 2 ^ { n + 1 } + 1 ) } $。
(1) 由题意知,$ a _ { 6 } = \frac { 2 ^ { 6 } } { 1 + 3 × 2 ^ { 6 } + 2 × ( 2 ^ { 6 } ) ^ { 2 } } = \frac { 1 } { 2 ^ { 6 } + 1 } - \frac { 1 } { 2 ^ { 7 } + 1 } $;
(2) $ a _ { n } = \frac { 2 ^ { n } } { 1 + 3 × 2 ^ { n } + 2 × ( 2 ^ { n } ) ^ { 2 } } = \frac { 1 } { 2 ^ { n } + 1 } - \frac { 1 } { 2 ^ { n + 1 } + 1 } $;
(3) 原式 $ = \frac { 1 } { 2 + 1 } - \frac { 1 } { 2 ^ { 2 } + 1 } + \frac { 1 } { 2 ^ { 2 } + 1 } - \frac { 1 } { 2 ^ { 3 } + 1 } + \frac { 1 } { 2 ^ { 3 } + 1 } - \frac { 1 } { 2 ^ { 4 } + 1 } + \frac { 1 } { 2 ^ { 4 } + 1 } - \frac { 1 } { 2 ^ { 5 } + 1 } + \frac { 1 } { 2 ^ { 5 } + 1 } - $
$ \frac { 1 } { 2 ^ { 6 } + 1 } + \frac { 1 } { 2 ^ { 6 } + 1 } - \frac { 1 } { 2 ^ { 7 } + 1 } = \frac { 1 } { 2 + 1 } - \frac { 1 } { 2 ^ { 7 } + 1 } = \frac { 14 } { 43 } $;
(4) 原式 $ = \frac { 1 } { 2 + 1 } - \frac { 1 } { 2 ^ { 2 } + 1 } + \frac { 1 } { 2 ^ { 2 } + 1 } - \frac { 1 } { 2 ^ { 3 } + 1 } + \cdots + \frac { 1 } { 2 ^ { n } + 1 } - \frac { 1 } { 2 ^ { n + 1 } + 1 } = \frac { 1 } { 2 + 1 } - \frac { 1 } { 2 ^ { n + 1 } + 1 } = $
$ \frac { 2 ^ { n + 1 } - 2 } { 3 ( 2 ^ { n + 1 } + 1 ) } $。
查看更多完整答案,请扫码查看


