2025年假期新思维七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期新思维七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
19. (7 分)为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图.

请根据以上两图解答下列问题:
(1)该班总人数是______;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.

请根据以上两图解答下列问题:
(1)该班总人数是______;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
答案:
解:
(1)由题意可知:
该班总人数是:$22÷55\% = 40$(人);
故答案为:40;
(2)由
(1)得,第四次优秀的人数为:$40×85\% = 34$(人),
第三次优秀率为:$\frac{32}{40}×100\% = 80\%$;
补全统计图如图所示:

(3)答案不唯一,如优秀人数逐渐增多,增大的幅度逐渐减小等。
解:
(1)由题意可知:
该班总人数是:$22÷55\% = 40$(人);
故答案为:40;
(2)由
(1)得,第四次优秀的人数为:$40×85\% = 34$(人),
第三次优秀率为:$\frac{32}{40}×100\% = 80\%$;
补全统计图如图所示:

(3)答案不唯一,如优秀人数逐渐增多,增大的幅度逐渐减小等。
20. (8 分)某校八年级全体 320 名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级. 为了了解电脑培训的效果,用抽签方式得到其中 32 名学生的两次考试考分等级,所绘制的统计图如所示.

试结合图示信息回答下列问题:
(1)这 32 名学生培训前考分的中位数所在的等级是
(2)这 32 名学生经过培训,考分等级“不合格”的百分比由
(3)估计该校整个八年级中,培训后考分等级为“合格”与“优秀”的学生共有
(4)你认为上述估计合理吗:理由是什么?
答:

试结合图示信息回答下列问题:
(1)这 32 名学生培训前考分的中位数所在的等级是
不合格
,培训后考分的中位数所在的等级是合格
.(2)这 32 名学生经过培训,考分等级“不合格”的百分比由
75%
下降到25%
.(3)估计该校整个八年级中,培训后考分等级为“合格”与“优秀”的学生共有
240
名.(4)你认为上述估计合理吗:理由是什么?
答:
不合理
,理由:因为该估计不能准确反映320名学生的成绩
.
答案:
解:
(1)这32名学生培训前考分的中位数所在的等级是不合格,培训后考分的中位数所在的等级是合格。故答案是:不合格,合格;
(2)培训前等级“不合格”的百分比是:$\frac{24}{32}×100\% = 75\%$,
培训后不合格的百分比是:$\frac{8}{32}×100\% = 25\%$;
故答案是75%、25%;
(3)$320×\frac{16 + 8}{32}=240$(名),
故答案是:240;
(4)不合理,因为该估计不能准确反映320名学生的成绩。
(1)这32名学生培训前考分的中位数所在的等级是不合格,培训后考分的中位数所在的等级是合格。故答案是:不合格,合格;
(2)培训前等级“不合格”的百分比是:$\frac{24}{32}×100\% = 75\%$,
培训后不合格的百分比是:$\frac{8}{32}×100\% = 25\%$;
故答案是75%、25%;
(3)$320×\frac{16 + 8}{32}=240$(名),
故答案是:240;
(4)不合理,因为该估计不能准确反映320名学生的成绩。
21. (江西中考)(9 分)为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
|种类|A|B|C|D|E|
|出行方式|共享单车|步行|公交车|的士|私家车|
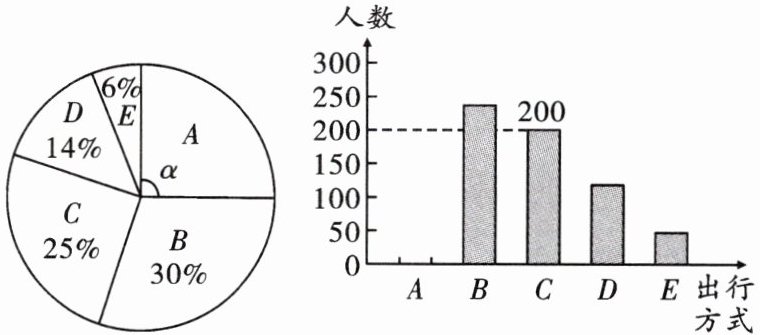
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有______人,其中选择 B 类的人数有______人;
(2)在扇形统计图中,求 A 类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有 12 万人出行,若将 A,B,C 这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
|种类|A|B|C|D|E|
|出行方式|共享单车|步行|公交车|的士|私家车|

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有______人,其中选择 B 类的人数有______人;
(2)在扇形统计图中,求 A 类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有 12 万人出行,若将 A,B,C 这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
答案:
解:
(1)本次调查的市民有$200÷25\% = 800$(人),
$\therefore B$类别的人数为$800×30\% = 240$(人),
故答案为:800,240;
(2)$\because A$类人数所占百分比为$1-(30\% + 25\% + 14\% + 6\%) = 25\%$,
$\therefore A$类对应扇形圆心角$\alpha$的度数为$360^{\circ}×25\% = 90^{\circ}$,A类的人数为$800×25\% = 200$(人),
补全条形图如下:

(3)$12×(25\% + 30\% + 25\%) = 9.6$(万人),
答:估计该市“绿色出行”方式的人数约为9.6万人。
解:
(1)本次调查的市民有$200÷25\% = 800$(人),
$\therefore B$类别的人数为$800×30\% = 240$(人),
故答案为:800,240;
(2)$\because A$类人数所占百分比为$1-(30\% + 25\% + 14\% + 6\%) = 25\%$,
$\therefore A$类对应扇形圆心角$\alpha$的度数为$360^{\circ}×25\% = 90^{\circ}$,A类的人数为$800×25\% = 200$(人),
补全条形图如下:

(3)$12×(25\% + 30\% + 25\%) = 9.6$(万人),
答:估计该市“绿色出行”方式的人数约为9.6万人。
查看更多完整答案,请扫码查看


