2025年假期新思维七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期新思维七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
8. 杨辉三角, 又称贾宪三角, 是二项式系数在三角形中的一种几何排列, 如图, 观察下面的杨辉三角:

按照前面的规律, 则 $(a + b)^5 = $

按照前面的规律, 则 $(a + b)^5 = $
$a ^ { 5 } + 5 a ^ { 4 } b + 10 a ^ { 3 } b ^ { 2 } + 10 a ^ { 2 } b ^ { 3 } + 5 a b ^ { 4 } + b ^ { 5 }$
.
答案:
$a ^ { 5 } + 5 a ^ { 4 } b + 10 a ^ { 3 } b ^ { 2 } + 10 a ^ { 2 } b ^ { 3 } + 5 a b ^ { 4 } + b ^ { 5 }$
9. 若关于 $x$ 的二次三项式 $x^2 + ax + \frac{1}{4}$ 是完全平方式, 则 $a$ 的值是
$\pm 1$
.
答案:
$\pm 1$
10. 发现任意五个连续整数的平方和是 5 的倍数.
验证 (1) $(-1)^2 + 0^2 + 1^2 + 2^2 + 3^2$ 的结果是 5 的几倍?
(2) 设五个连续整数的中间一个为 $n$, 写出它们的平方和, 并说明是 5 的倍数.
延伸 三个连续整数的平方和被 3 除的余数是 2.
验证 (1) $(-1)^2 + 0^2 + 1^2 + 2^2 + 3^2$ 的结果是 5 的几倍?
(2) 设五个连续整数的中间一个为 $n$, 写出它们的平方和, 并说明是 5 的倍数.
延伸 三个连续整数的平方和被 3 除的余数是 2.
答案:
解: 验证
(1) $( - 1 ) ^ { 2 } + 0 ^ { 2 } + 1 ^ { 2 } + 2 ^ { 2 } + 3 ^ { 2 } = 1 + 0 + 1 + 4 + 9 = 15$,$15 ÷ 5 = 3$,即 $( - 1 ) ^ { 2 } + 0 ^ { 2 } + 1 ^ { 2 } + 2 ^ { 2 } + 3 ^ { 2 }$ 的结果是 5 的 3 倍;
(2) 设五个连续整数的中间一个为 $n$,则其余的 4 个整数分别是 $n - 2$,$n - 1$,$n + 1$,$n + 2$,它们的平方和为: $( n - 2 ) ^ { 2 } + ( n - 1 ) ^ { 2 } + n ^ { 2 } + ( n + 1 ) ^ { 2 } + ( n + 2 ) ^ { 2 } = n ^ { 2 } - 4 n + 4 + n ^ { 2 } - 2 n + 1 + n ^ { 2 } + n ^ { 2 } + 2 n + 1 + n ^ { 2 } + 4 n + 4 = 5 n ^ { 2 } + 10$,
$\because 5 n ^ { 2 } + 10 = 5 ( n ^ { 2 } + 2 )$,
又 $n$ 是整数,$\therefore n ^ { 2 } + 2$ 是整数,
$\therefore$ 五个连续整数的平方和是 5 的倍数;
延伸 设三个连续整数的中间一个为 $n$,则其余的 2 个整数是 $n - 1$,$n + 1$,
它们的平方和为: $( n - 1 ) ^ { 2 } + n ^ { 2 } + ( n + 1 ) ^ { 2 }$
$ = n ^ { 2 } - 2 n + 1 + n ^ { 2 } + n ^ { 2 } + 2 n + 1 = 3 n ^ { 2 } + 2$,
$\because n$ 是整数,$\therefore n ^ { 2 }$ 是整数,
$\therefore$ 任意三个连续整数的平方和被 3 除的余数是 2.
(1) $( - 1 ) ^ { 2 } + 0 ^ { 2 } + 1 ^ { 2 } + 2 ^ { 2 } + 3 ^ { 2 } = 1 + 0 + 1 + 4 + 9 = 15$,$15 ÷ 5 = 3$,即 $( - 1 ) ^ { 2 } + 0 ^ { 2 } + 1 ^ { 2 } + 2 ^ { 2 } + 3 ^ { 2 }$ 的结果是 5 的 3 倍;
(2) 设五个连续整数的中间一个为 $n$,则其余的 4 个整数分别是 $n - 2$,$n - 1$,$n + 1$,$n + 2$,它们的平方和为: $( n - 2 ) ^ { 2 } + ( n - 1 ) ^ { 2 } + n ^ { 2 } + ( n + 1 ) ^ { 2 } + ( n + 2 ) ^ { 2 } = n ^ { 2 } - 4 n + 4 + n ^ { 2 } - 2 n + 1 + n ^ { 2 } + n ^ { 2 } + 2 n + 1 + n ^ { 2 } + 4 n + 4 = 5 n ^ { 2 } + 10$,
$\because 5 n ^ { 2 } + 10 = 5 ( n ^ { 2 } + 2 )$,
又 $n$ 是整数,$\therefore n ^ { 2 } + 2$ 是整数,
$\therefore$ 五个连续整数的平方和是 5 的倍数;
延伸 设三个连续整数的中间一个为 $n$,则其余的 2 个整数是 $n - 1$,$n + 1$,
它们的平方和为: $( n - 1 ) ^ { 2 } + n ^ { 2 } + ( n + 1 ) ^ { 2 }$
$ = n ^ { 2 } - 2 n + 1 + n ^ { 2 } + n ^ { 2 } + 2 n + 1 = 3 n ^ { 2 } + 2$,
$\because n$ 是整数,$\therefore n ^ { 2 }$ 是整数,
$\therefore$ 任意三个连续整数的平方和被 3 除的余数是 2.
11. 规定两数 $a, b$ 之间的一种运算, 记作 $(a, b)$: 如果 $a^c = b$, 那么 $(a, b) = c$.
例如: 因为 $2^3 = 8$, 所以 $(2, 8) = 3$.
(1) 根据上述规定, 填空:
$(3, 27) = $
(2) 小明在研究这种运算时发现一个现象: $(3^n, 4^n) = (3, 4)$, 小明给出了如下的证明:
设 $(3^n, 4^n) = x$, 则 $(3^n)^x = 4^n$, 即 $(3^x)^n = 4^n$.
所以 $3^x = 4$, 即 $(3, 4) = x$, 所以 $(3^n, 4^n) = (3, 4)$.
请你尝试运用这种方法证明下面这个等式: $(3, 4) + (3, 5) = (3, 20)$.
例如: 因为 $2^3 = 8$, 所以 $(2, 8) = 3$.
(1) 根据上述规定, 填空:
$(3, 27) = $
3
, $(5, 1) = $0
, $(2, \frac{1}{4}) = $-2
.(2) 小明在研究这种运算时发现一个现象: $(3^n, 4^n) = (3, 4)$, 小明给出了如下的证明:
设 $(3^n, 4^n) = x$, 则 $(3^n)^x = 4^n$, 即 $(3^x)^n = 4^n$.
所以 $3^x = 4$, 即 $(3, 4) = x$, 所以 $(3^n, 4^n) = (3, 4)$.
请你尝试运用这种方法证明下面这个等式: $(3, 4) + (3, 5) = (3, 20)$.
答案:
(1) 解: $\because 3 ^ { 3 } = 27$,$\therefore ( 3,27 ) = 3$;$\because 5 ^ { 0 } = 1$,$\therefore ( 5,1 ) = 0$;$\because 2 ^ { - 2 } = \frac { 1 } { 4 }$,$\therefore ( 2, \frac { 1 } { 4 } ) = - 2$;
(2) 证明: 设 $( 3,4 ) = x$,$( 3,5 ) = y$,则 $3 ^ { x } = 4$,$3 ^ { y } = 5$,$\therefore 3 ^ { x + y } = 3 ^ { x } \cdot 3 ^ { y } = 20$,$\therefore ( 3,20 ) = x + y$,$\therefore ( 3,4 ) + ( 3,5 ) = ( 3,20 )$.
(1) 解: $\because 3 ^ { 3 } = 27$,$\therefore ( 3,27 ) = 3$;$\because 5 ^ { 0 } = 1$,$\therefore ( 5,1 ) = 0$;$\because 2 ^ { - 2 } = \frac { 1 } { 4 }$,$\therefore ( 2, \frac { 1 } { 4 } ) = - 2$;
(2) 证明: 设 $( 3,4 ) = x$,$( 3,5 ) = y$,则 $3 ^ { x } = 4$,$3 ^ { y } = 5$,$\therefore 3 ^ { x + y } = 3 ^ { x } \cdot 3 ^ { y } = 20$,$\therefore ( 3,20 ) = x + y$,$\therefore ( 3,4 ) + ( 3,5 ) = ( 3,20 )$.
12. (1) 问题再现
数形结合是解决数学问题的一种重要的思想方法, 借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性, 从而可以帮助我们快速解题. 初中数学里的一些代数公式, 很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如: 利用图形的几何意义证明完全平方公式.
证明: 将一个边长为 $a$ 的正方形的边长增加 $b$, 形成两个长方形和两个正方形, 如图 1:
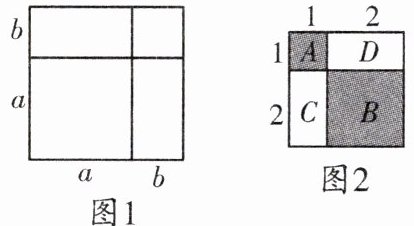
这个图形的面积可以表示成:
$(a + b)^2$ 或 $a^2 + 2ab + b^2$
$\therefore (a + b)^2 = a^2 + 2ab + b^2$
这就验证了两数和的完全平方公式.
类比解决 请你类比上述方法, 利用图形的几何意义证明平方差公式. (要求画出图形并写出推理过程)
(2) 问题提出
如何利用图形几何意义的方法证明: $1^3 + 2^3 = 3^2$?
如图 2, $A$ 表示 1 个 $1 × 1$ 的正方形, 即: $1 × 1 × 1 = 1^3$,
$B$ 表示 1 个 $2 × 2$ 的正方形, $C$ 与 $D$ 恰好可以拼成 1 个 $2 × 2$ 的正方形, 因此: $B$、$C$、$D$ 就可以表示 2 个 $2 × 2$ 的正方形, 即: $2 × 2 × 2 = 2^3$,
而 $A$、$B$、$C$、$D$ 恰好可以拼成一个 $(1 + 2) × (1 + 2)$ 的大正方形.
由此可得: $1^3 + 2^3 = (1 + 2)^2 = 3^2$,
尝试解决 请你类比上述推导过程, 利用图形的几何意义确定: $1^3 + 2^3 + 3^3 = $____. (要求写出结论并构造图形写出推证过程).
(3) 问题拓展
请用上面的表示几何图形面积的方法探究: $1^3 + 2^3 + 3^3 + … + n^3 = $____. (直接写出结论即可, 不必写出解题过程)
数形结合是解决数学问题的一种重要的思想方法, 借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性, 从而可以帮助我们快速解题. 初中数学里的一些代数公式, 很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如: 利用图形的几何意义证明完全平方公式.
证明: 将一个边长为 $a$ 的正方形的边长增加 $b$, 形成两个长方形和两个正方形, 如图 1:

这个图形的面积可以表示成:
$(a + b)^2$ 或 $a^2 + 2ab + b^2$
$\therefore (a + b)^2 = a^2 + 2ab + b^2$
这就验证了两数和的完全平方公式.
类比解决 请你类比上述方法, 利用图形的几何意义证明平方差公式. (要求画出图形并写出推理过程)
(2) 问题提出
如何利用图形几何意义的方法证明: $1^3 + 2^3 = 3^2$?
如图 2, $A$ 表示 1 个 $1 × 1$ 的正方形, 即: $1 × 1 × 1 = 1^3$,
$B$ 表示 1 个 $2 × 2$ 的正方形, $C$ 与 $D$ 恰好可以拼成 1 个 $2 × 2$ 的正方形, 因此: $B$、$C$、$D$ 就可以表示 2 个 $2 × 2$ 的正方形, 即: $2 × 2 × 2 = 2^3$,
而 $A$、$B$、$C$、$D$ 恰好可以拼成一个 $(1 + 2) × (1 + 2)$ 的大正方形.
由此可得: $1^3 + 2^3 = (1 + 2)^2 = 3^2$,
尝试解决 请你类比上述推导过程, 利用图形的几何意义确定: $1^3 + 2^3 + 3^3 = $____. (要求写出结论并构造图形写出推证过程).
(3) 问题拓展
请用上面的表示几何图形面积的方法探究: $1^3 + 2^3 + 3^3 + … + n^3 = $____. (直接写出结论即可, 不必写出解题过程)
答案:
解:
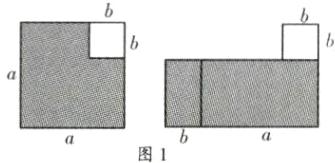
(1) $\because$ 如图 1 的阴影部分的面积是 $a ^ { 2 } - b ^ { 2 }$,图 4 的阴影部分的面积是 $( a + b ) ( a - b )$,
$\therefore a ^ { 2 } - b ^ { 2 } = ( a + b ) ( a - b )$,
这就验证了平方差公式;
(2) 如图 2,$A$ 表示 1 个 $1 × 1$ 的正方形,即 $1× 1 × 1 = 1 ^ { 3 }$;$B$ 表示 1 个 $2 × 2$ 的正方形,$C$ 与 $D$ 恰好可以拼成 1 个 $2 × 2$ 的正方形,因此 $B$、$C$、$D$ 就可以表示 2 个 $2 × 2$ 的正方形,
即: $2 × 2 × 2 = 2 ^ { 3 }$;$G$ 与 $H$,$E$ 与 $F$ 可以表示 2 个 $3 × 3$ 的正方形,$I$ 表示 1 个 $3 × 3$ 的正方形,因此 $E$、$F$、$G$、$H$、$I$ 可以表示 3 个 $3 × 3$ 的正方形,因此: $3 × 3 × 3 = 3 ^ { 3 }$. 而整个图形恰好可以拼成一个 $( 1 + 2 + 3 ) × ( 1 + 2 + 3 )$ 的大正方形,由此可得: $1 ^ { 3 } + 2 ^ { 3 } + 3 ^ { 3 } = ( 1 + 2 + 3 ) ^ { 2 } = 6 ^ { 2 }$;
(3) $ \left[ \frac { 1 } { 2 } n ( n + 1 ) \right] ^ { 2 }$.

解:
(1) $\because$ 如图 1 的阴影部分的面积是 $a ^ { 2 } - b ^ { 2 }$,图 4 的阴影部分的面积是 $( a + b ) ( a - b )$,
$\therefore a ^ { 2 } - b ^ { 2 } = ( a + b ) ( a - b )$,
这就验证了平方差公式;
(2) 如图 2,$A$ 表示 1 个 $1 × 1$ 的正方形,即 $1× 1 × 1 = 1 ^ { 3 }$;$B$ 表示 1 个 $2 × 2$ 的正方形,$C$ 与 $D$ 恰好可以拼成 1 个 $2 × 2$ 的正方形,因此 $B$、$C$、$D$ 就可以表示 2 个 $2 × 2$ 的正方形,
即: $2 × 2 × 2 = 2 ^ { 3 }$;$G$ 与 $H$,$E$ 与 $F$ 可以表示 2 个 $3 × 3$ 的正方形,$I$ 表示 1 个 $3 × 3$ 的正方形,因此 $E$、$F$、$G$、$H$、$I$ 可以表示 3 个 $3 × 3$ 的正方形,因此: $3 × 3 × 3 = 3 ^ { 3 }$. 而整个图形恰好可以拼成一个 $( 1 + 2 + 3 ) × ( 1 + 2 + 3 )$ 的大正方形,由此可得: $1 ^ { 3 } + 2 ^ { 3 } + 3 ^ { 3 } = ( 1 + 2 + 3 ) ^ { 2 } = 6 ^ { 2 }$;
(3) $ \left[ \frac { 1 } { 2 } n ( n + 1 ) \right] ^ { 2 }$.


查看更多完整答案,请扫码查看


