《2025年假期新思维七年级数学北师大版》

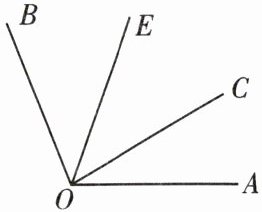
15. (6 分)已知 $ O C $ 是 $ \angle A O B $ 内部的一条射线,$ \angle A O C = 30 ^ { \circ } $,$ O E $ 是 $ \angle C O B $ 的平分线,当 $ \angle C O E = 40 ^ { \circ } $ 时,求 $ \angle A O B $ 的度数.

答案： 解：
∵OE是∠COB的平分线
∴∠COB=2∠COE（角平分线定义）
∵∠COE=40°
∴∠COB=2×40°=80°
∵∠AOC=30°
∴∠AOB=∠AOC+∠COB=30°+80°=110°
答：∠AOB的度数为110°。

16. (6 分)如图,已知点 $ C $ 为 $ A B $ 上一点,$ A C = 15 \mathrm { cm } $,$ C B = \frac { 2 } { 3 } A C $,若 $ D $、$ E $ 分别为 $ A C $、$ A B $ 的中点,求 $ D E $ 的长.

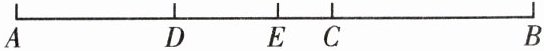
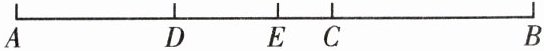
答案： 解：
∵AC=15cm，CB=$\frac{2}{3}$AC，
∴CB=$\frac{2}{3}$×15=10cm，
∴AB=AC+CB=15+10=25cm。
∵D是AC的中点，E是AB的中点，
∴AD=$\frac{1}{2}$AC=$\frac{1}{2}$×15=7.5cm，
AE=$\frac{1}{2}$AB=$\frac{1}{2}$×25=12.5cm，
∴DE=AE-AD=12.5-7.5=5cm。
答：DE的长为5cm。

17. (6 分)如图,已知四点 $ A $、$ B $、$ C $、$ D $,请用尺规作图完成.(保留画图痕迹)
(1)画直线 $ A B $；
(2)画射线 $ A C $；
(3)连接 $ B C $ 并延长 $ B C $ 到 $ E $,使得 $ C E = A B + B C $；
(4)在线段 $ B D $ 上取点 $ P $,使 $ P A + P C $ 的值最小.

答案：
解：（1）直线AB如图所示；
（2）射线AC如图所示；
（3）线段BC、CE如图所示；
（4）线段BD、点P如图所示。

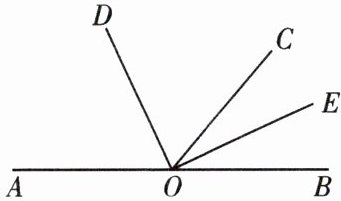
18. (7 分)如图,点 $ A $,$ O $,$ B $ 在同一条直线上,$ O D $,$ O E $ 分别平分 $ \angle A O C $ 和 $ \angle B O C $.
(1)求 $ \angle D O E $ 的度数；
(2)如果 $ \angle C O D = 65 ^ { \circ } $,求 $ \angle A O E $ 的度数.

答案： 解：（1）
∵OD是∠AOC的平分线，
∴∠COD=$\frac{1}{2}$∠AOC。
∵OE是∠BOC的平分线，
∴∠COE=$\frac{1}{2}$∠BOC。所以∠DOE=∠COD+∠COE=$\frac{1}{2}$(∠AOC + ∠BOC)=$\frac{1}{2}$∠AOB = 90°。
（2）由（1）可知：∠BOE=∠COE=90°−∠COD = 25°，所以∠AOE=180°−∠BOE = 155°。

19. (7 分)已知 $ m $,$ n $ 满足算式 $ ( m - 6 ) ^ { 2 } + | n - 2 | = 0 $.
(1)求 $ m $,$ n $ 的值；
(2)已知线段 $ A B = m $,在直线 $ A B $ 上取一点 $ P $,恰好使 $ A P = n P B $,点 $ Q $ 为 $ P B $ 的中点,求线段 $ A Q $ 的长.

答案： 解：（1）由条件可得$(m−6)^2 = 0$，$\vert n−2\vert = 0$，所以m = 6，n = 2。
（2）当点P在线段AB之间时，AP = 2PB，所以AP = 4，PB = 2，而Q为PB的中点，所以PQ = 1，故AQ = AP + PQ = 5。当点P在线段AB的延长线上时，AP−PB = AB，即2PB−PB = 6，所以PB = 6，而Q为PB的中点，所以BQ = 3，AQ = AB + BQ = 6 + 3 = 9，故线段AQ的长为5或9。

20. (8 分)如图,$ B $ 是线段 $ A D $ 上一动点,沿 $ A \to D \to A $ 以 $ 2 \mathrm { cm } / \mathrm { s } $ 的速度往返运动 $ 1 $ 次,$ C $ 是线段 $ B D $ 的中点,$ A D = 10 \mathrm { cm } $,设点 $ B $ 运动时间为 $ t $ 秒 $ ( 0 \leq t \leq 10 ) $.
(1)当 $ t = 2 $ 时,①$ A B = $______4$ \mathrm { cm } $. ②求线段 $ C D $ 的长度.
(2)用含 $ t $ 的代数式表示运动过程中 $ A B $ 的长.
(3)在运动过程中,若 $ A B $ 中点为 $ E $,则 $ E C $ 的长是否变化？若不变,求出 $ E C $ 的长；若发生变化,请说明理由.

答案： 解：（1）①
∵B是线段AD上一动点，沿A→D→A以2cm/s的速度往返运动，
∴当t = 2时，AB = 2×2 = 4cm。故答案为：4；
②
∵AD = 10cm，AB = 4cm，
∴BD = 10−4 = 6cm，
∵C是线段BD的中点，
∴CD=$\frac{1}{2}$BD=$\frac{1}{2}$×6 = 3cm；
（2）
∵B是线段AD上一动点，沿A→D→A以2cm/s的速度往返运动，
∴当0≤t≤5时，AB = 2t；当5 ＜ t≤10时，AB = 10−(2t−10)=20−2t；
（3）不变。
∵AB中点为E，C是线段BD的中点，
∴EC=$\frac{1}{2}$(AB + BD)=$\frac{1}{2}$AD=$\frac{1}{2}$×10 = 5cm。