2025年假期新思维七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年假期新思维七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 三角形的有关概念
(1) 定义: 由不在同一直线上的三条线段首尾顺次连接所组成的图形叫做
注意: 由三角形的定义可知, 三角形有三个特征: ①三条线段; ②不在同一直线上; ③首尾顺次连接, 这是识别三角形的依据.
(2) 数三角形个数的方法: ①按图形形成的过程(即重新画一遍图形, 按照三角形形成的先后顺序去数); ②按大小顺序; ③可从图中的某一条线段开始沿着一定方向去数; ④先固定一个顶点, 变换另两个顶点来数.
(1) 定义: 由不在同一直线上的三条线段首尾顺次连接所组成的图形叫做
三角形
.注意: 由三角形的定义可知, 三角形有三个特征: ①三条线段; ②不在同一直线上; ③首尾顺次连接, 这是识别三角形的依据.
(2) 数三角形个数的方法: ①按图形形成的过程(即重新画一遍图形, 按照三角形形成的先后顺序去数); ②按大小顺序; ③可从图中的某一条线段开始沿着一定方向去数; ④先固定一个顶点, 变换另两个顶点来数.
答案:
1. 三角形
2. 三角形的分类
(1) 按边分类
三角形$\begin{cases}不等边三角形\\等腰三角形\begin{cases}腰与底不相等的等腰三角形\\腰与底相等的等边三角形\end{cases} \end{cases}$
(2) 按角分类
三角形$\begin{cases}直角三角形\\斜三角形\begin{cases}锐角三角形\\钝角三角形\end{cases} \end{cases}$
注意: 边和角都特殊的三角形(既等腰又直角), 叫做______.
(1) 按边分类
三角形$\begin{cases}不等边三角形\\等腰三角形\begin{cases}腰与底不相等的等腰三角形\\腰与底相等的等边三角形\end{cases} \end{cases}$
(2) 按角分类
三角形$\begin{cases}直角三角形\\斜三角形\begin{cases}锐角三角形\\钝角三角形\end{cases} \end{cases}$
注意: 边和角都特殊的三角形(既等腰又直角), 叫做______.
答案:
2. 等腰直角三角形
3. 三角形三边的关系
(1) 两边之和______第三边, 两边之差______第三边.
(2) 三边关系的依据是: 两点之间线段______.
(3) 判断三条线段能否构成三角形的方法: 只要满足较小的两条线段之和______第三条线段, 便可构成三角形; 若不满足, 则不能构成三角形.
(4) 三角形第三边的取值范围是: 两边之差______第三边______两边之和.
(1) 两边之和______第三边, 两边之差______第三边.
(2) 三边关系的依据是: 两点之间线段______.
(3) 判断三条线段能否构成三角形的方法: 只要满足较小的两条线段之和______第三条线段, 便可构成三角形; 若不满足, 则不能构成三角形.
(4) 三角形第三边的取值范围是: 两边之差______第三边______两边之和.
答案:
3.
(1) 大于 小于
(2) 最短
(3) 大于
(4) < <
(1) 大于 小于
(2) 最短
(3) 大于
(4) < <
4. 三角形的高
(1) 定义: 从三角形的一个顶点向它的对边作一条垂线, ______和______之间的线段叫做三角形的高线, 简称三角形的高.
(2) 性质: 如图, 若$AD是\triangle ABC$的高, 则$\angle ADC= $______.
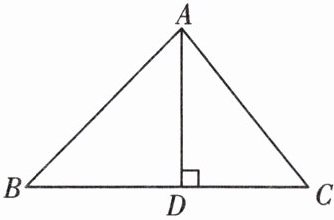
(3) 三角形三条高线交点的位置
①锐角三角形三条高线的交点在三角形的______.
②直角三角形三条高线的交点是______.
③钝角三角形三条高线的交点在三角形的______.
(1) 定义: 从三角形的一个顶点向它的对边作一条垂线, ______和______之间的线段叫做三角形的高线, 简称三角形的高.
(2) 性质: 如图, 若$AD是\triangle ABC$的高, 则$\angle ADC= $______.

(3) 三角形三条高线交点的位置
①锐角三角形三条高线的交点在三角形的______.
②直角三角形三条高线的交点是______.
③钝角三角形三条高线的交点在三角形的______.
答案:
4.
(1) 顶点 垂足
(2) $ 90^{\circ} $
(3) ① 内部 ② 直角顶点 ③ 外部
(1) 顶点 垂足
(2) $ 90^{\circ} $
(3) ① 内部 ② 直角顶点 ③ 外部
5. 三角形的中线
(1) 定义: 在三角形中, 连接一个顶点与它对边的______的线段, 叫做这个三角形的中线, 三角形三条中线的交点叫做______.
(2) ①性质: 如图, 若$AD是\triangle ABC$的中线, 则$BD= $______.
②三角形的中线能将三角形分成面积相等的两部分, 即若$AD是\triangle ABC$的中线, 即$S_{\triangle CAD}= $______$=\frac{1}{2}S_{\triangle ABC}$.

(1) 定义: 在三角形中, 连接一个顶点与它对边的______的线段, 叫做这个三角形的中线, 三角形三条中线的交点叫做______.
(2) ①性质: 如图, 若$AD是\triangle ABC$的中线, 则$BD= $______.
②三角形的中线能将三角形分成面积相等的两部分, 即若$AD是\triangle ABC$的中线, 即$S_{\triangle CAD}= $______$=\frac{1}{2}S_{\triangle ABC}$.

答案:
5.
(1) 中点 三角形的重心
(2) ① $ DC $ ② $ S_{\triangle ADB} $
(1) 中点 三角形的重心
(2) ① $ DC $ ② $ S_{\triangle ADB} $
6. 三角形的角平分线
(1) 定义: 在三角形中, 一个内角的平分线与它的对边相交, 则这个角的______叫做三角形的角平分线.
(2) 性质: 如图, 若$AD是\triangle ABC$的角平分线, 则有$\angle 1= $______$=$______.

(1) 定义: 在三角形中, 一个内角的平分线与它的对边相交, 则这个角的______叫做三角形的角平分线.
(2) 性质: 如图, 若$AD是\triangle ABC$的角平分线, 则有$\angle 1= $______$=$______.

答案:
6.
(1) 顶点与交点之间的线段
(2) $ ∠2 $ $ \frac{1}{2}∠BAC $
(1) 顶点与交点之间的线段
(2) $ ∠2 $ $ \frac{1}{2}∠BAC $
7. 三角形的稳定性
三角形具有______, 四边形具有______. 在工程建筑中为使建筑物稳定常采用______结构, 而银行的活动门都是用______结构.
三角形具有______, 四边形具有______. 在工程建筑中为使建筑物稳定常采用______结构, 而银行的活动门都是用______结构.
答案:
7. 稳定性 不稳定性 三角形 四边形
8. 三角形的内角
三角形的内角和定理: ______.
三角形的内角和定理: ______.
答案:
8. 三角形的内角和等于 $ 180^{\circ} $
9. 全等形的概念
能够______的两个图形叫做全等形. 平移、翻折、旋转前后的图形全等.
能够______的两个图形叫做全等形. 平移、翻折、旋转前后的图形全等.
答案:
9. 完全重合
10. 全等三角形
(1) 定义: 能够______的两个三角形叫做全等三角形.
(2) 对应元素: 两个全等三角形重合时, 互相重合的顶点叫做______, 互相重合的边叫做______, 互相重合的角叫做______.
(3) 表示方法: $\triangle ABC和\triangle DEF$全等记作______.(通常要求把表示对应顶点的字母写在对应的位置上)
(4) 性质: 全等三角形的对应边______, 对应角______.
(1) 定义: 能够______的两个三角形叫做全等三角形.
(2) 对应元素: 两个全等三角形重合时, 互相重合的顶点叫做______, 互相重合的边叫做______, 互相重合的角叫做______.
(3) 表示方法: $\triangle ABC和\triangle DEF$全等记作______.(通常要求把表示对应顶点的字母写在对应的位置上)
(4) 性质: 全等三角形的对应边______, 对应角______.
答案:
10.
(1) 完全重合
(2) 对应点 对应边 对应角
(3) $ \triangle ABC \cong \triangle DEF $
(4) 相等 相等
(1) 完全重合
(2) 对应点 对应边 对应角
(3) $ \triangle ABC \cong \triangle DEF $
(4) 相等 相等
11. 全等三角形的判定方法
(1) 判定$1$: 三边对应______的两个三角形全
(2) 判定$2$: ______的两个三角形全等, 可以简写成: $SAS$.
(3) 判定$3$: ______的两个三角形全等, 可以简写成: $AAS$.
(4) 判定$4$: ______的两个三角形全等, 可以简写成: $ASA$.
(5) 判定$5$: ______的两个直角三角形全等, 可以简写成: $HL$.
(1) 判定$1$: 三边对应______的两个三角形全
等
, 可以简写成: ______.(2) 判定$2$: ______的两个三角形全等, 可以简写成: $SAS$.
(3) 判定$3$: ______的两个三角形全等, 可以简写成: $AAS$.
(4) 判定$4$: ______的两个三角形全等, 可以简写成: $ASA$.
(5) 判定$5$: ______的两个直角三角形全等, 可以简写成: $HL$.
答案:
11.
(1) 相等 $ SSS $
(2) 两边和它们的夹角分别相等
(3) 两角和其中一角的对边分别相等
(4) 两角和它们的夹边分别相等
(5) 一条直角边和斜边对应相等
(1) 相等 $ SSS $
(2) 两边和它们的夹角分别相等
(3) 两角和其中一角的对边分别相等
(4) 两角和它们的夹边分别相等
(5) 一条直角边和斜边对应相等
12. 角平分线
(1) 角平分线性质定理: 角平分线上的点到这个角两边的距离______.
(2) 逆定理: 到一个角两边的距离相等的点在______.
(1) 角平分线性质定理: 角平分线上的点到这个角两边的距离______.
(2) 逆定理: 到一个角两边的距离相等的点在______.
答案:
12.
(1) 相等
(2) 这个角的平分线上
(1) 相等
(2) 这个角的平分线上
13. 尺规作图
(1) 作一个角等于已知角
已知: $\angle AOB$
求作: $\angle A'O'B'$, 使$\angle A'O'B'= \angle AOB$

作法: ①以点$O$为圆心, ______为半径画弧, 分别交$OA$,$OB于点C$,$D$;
②画一条射线$O'A'$, 以点______为圆心, ______长为半径画弧, 交$O'A'于点C'$.
③以点______为圆心, ______长为半径画弧, 与第②步中所画的弧相交于点$D'$;
④过点$D'画射线O'B'$, 则$\angle A'O'B'= \angle AOB$.
注意: 明确三次画弧的圆心、半径.
(2) 作已知角的平分线
已知: $\angle AOB$
求作: $\angle AOB$的平分线

作法: ①以点______为圆心, ______为半径画弧, 交$OA于点M$, 交$OB于点N$.
②分别以点______为圆心, ______的长为半径画弧. 两弧在$\angle AOB的内部相交于点C$.
③画射线$OC$, 射线$OC$为所求.
(1) 作一个角等于已知角
已知: $\angle AOB$
求作: $\angle A'O'B'$, 使$\angle A'O'B'= \angle AOB$

作法: ①以点$O$为圆心, ______为半径画弧, 分别交$OA$,$OB于点C$,$D$;
②画一条射线$O'A'$, 以点______为圆心, ______长为半径画弧, 交$O'A'于点C'$.
③以点______为圆心, ______长为半径画弧, 与第②步中所画的弧相交于点$D'$;
④过点$D'画射线O'B'$, 则$\angle A'O'B'= \angle AOB$.
注意: 明确三次画弧的圆心、半径.
(2) 作已知角的平分线
已知: $\angle AOB$
求作: $\angle AOB$的平分线

作法: ①以点______为圆心, ______为半径画弧, 交$OA于点M$, 交$OB于点N$.
②分别以点______为圆心, ______的长为半径画弧. 两弧在$\angle AOB的内部相交于点C$.
③画射线$OC$, 射线$OC$为所求.
答案:
13.
(1) ① 任意长 ② $ O' $ $ OC $ ③ $ C' $ $ CD $
(2) ① $ O $ 适当长 ② $ M $,$ N $ 大于 $ \frac{1}{2}MN $
(1) ① 任意长 ② $ O' $ $ OC $ ③ $ C' $ $ CD $
(2) ① $ O $ 适当长 ② $ M $,$ N $ 大于 $ \frac{1}{2}MN $
查看更多完整答案,请扫码查看


