《2025年假期新思维七年级数学北师大版》

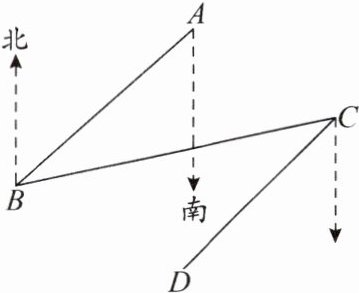
18. (7分)如图,$ B $ 处在 $ A $ 处的南偏西 $ 45^\circ $ 方向,$ C $ 处在 $ B $ 处的北偏东 $ 80^\circ $ 方向。
(1)求 $ \angle ABC $ 的度数。
(2)要使 $ CD // AB $,$ D $ 处应在 $ C $ 处的什么方向？

答案： 解：
(1)$\angle ABC = 80° - 45° = 35°$
(2)要使三条道路$CD// AB$，D处应平移到C处的南偏西45°的方向，此时空白部分的面积（即蔬菜的总种植面积）不变，因此蔬菜的总种植面积为$(20 - 2)×(32 - 1) = 558(m^2)$。

19. (7分)张三打算在院子里种上蔬菜,已知院子为东西长 $ 32 \text{ m} $,南北宽 $ 20 \text{ m} $ 的长方形。为了行走方便,要修筑同样宽的三条道路：东西两条,南北一条。南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、菜豆、黄瓜等蔬菜,若每条道路的宽均为 $ 1 \text{ m} $,求蔬菜的总种植面积是多少？

答案： 解：院子总面积为 $32 × 20 = 640 \, \text{m}^2$。
东西道路两条，每条宽 $1 \, \text{m}$，长 $32 \, \text{m}$，面积为 $2 × 32 × 1 = 64 \, \text{m}^2$。
南北道路一条，宽 $1 \, \text{m}$，长 $20 \, \text{m}$，面积为 $20 × 1 = 20 \, \text{m}^2$。
重叠部分为 $2$ 个边长 $1 \, \text{m}$ 的正方形，面积为 $2 × 1 × 1 = 2 \, \text{m}^2$。
道路总面积为 $64 + 20 - 2 = 82 \, \text{m}^2$。
蔬菜种植面积为 $640 - 82 = 558 \, \text{m}^2$。
答：蔬菜的总种植面积是 $558 \, \text{m}^2$。

20. (8分)如图,已知射线 $ AB $ 与直线 $ CD $ 交于点 $ O $,$ OF $ 平分 $ \angle BOC $,$ OG \perp OF $ 于 $ O $,$ AE // OF $,且 $ \angle A = 30^\circ $。
(1)求 $ \angle DOF $ 的度数；
(2)试说明 $ OD $ 平分 $ \angle AOG $。

答案： 解：
(1)$\because AE// OF$，$\therefore \angle FOB = \angle A = 30°$，$\because OF$平分$\angle BOC$，
$\therefore \angle COF = \angle FOB = 30°$，$\therefore \angle DOF = 180° - \angle COF = 150°$；
(2)$\because OF\perp OG$，$\therefore \angle FOG = 90°$，$\therefore \angle DOG = \angle DOF - \angle FOG = 150° - 90° = 60°$，$\because \angle AOD = \angle COB = \angle COF + \angle FOB = 60°$，
$\therefore \angle AOD = \angle DOG$，$\therefore OD$平分$\angle AOG$。

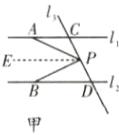
21. (9分)如图,已知直线 $ l_1 // l_2 $,直线 $ l_3 $ 和直线 $ l_1 $、$ l_2 $ 分别交于点 $ C $、$ D $,在线段 $ CD $ 上有一点 $ P $。
(1)如果点 $ P $ 在点 $ C $、$ D $ 之间运动,问 $ \angle PAC $、$ \angle APB $、$ \angle PBD $ 之间的关系是否发生变化；
(2)若点 $ P $ 在 $ C $、$ D $ 两点的外侧运动时(点 $ P $ 与点 $ C $、$ D $ 不重合),试探索 $ \angle PAC $、$ \angle APB $、$ \angle PBD $ 之间的关系又是如何？

答案：
解：
(1)不变，$\angle APB = \angle PAC + \angle PBD$。
理由：如图甲，过点P作$PE// l_1$，
则$\angle APE = \angle PAC$（两直线平行，内错角相等）。
又$\because l_1// l_2$，
$\therefore PE// l_2$（平行定理的推论），
$\therefore \angle BPE = \angle PBD$（两直线平行，内错角相等）。
$\therefore \angle APE + \angle BPE = \angle PAC + \angle PBD$，
即$\angle APB = \angle PAC + \angle PBD$。

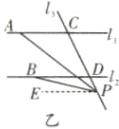
(2)若点P在C、D两点的外侧运动时（点P与点C、D不重合），则有两种情形：
①如图乙，有结论：$\angle APB = \angle PAC - \angle PBD$。
理由：过点P作$PE// l_1$，
则$\angle PAC = \angle APE$（两直线平行，内错角相等）。
又$\because l_1// l_2$，
$\therefore PE// l_2$（平行定理的推论），
$\therefore \angle BPE = \angle PBD$（两直线平行，内错角相等），$\therefore \angle APB = \angle APE - \angle BPE$，即$\angle APB = \angle PAC - \angle PBD$。


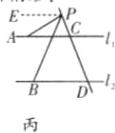
②如图丙，有结论：$\angle APB = \angle PBD - \angle PAC$。
理由：过点P作$PE// l_2$，则$\angle BPE = \angle PBD$（两直线平行，内错角相等）。又$\because l_1// l_2$，
$\therefore PE// l_1$（平行定理的推论），$\therefore \angle APE = \angle PAC$（两直线平行，内错角相等），$\therefore \angle APB = \angle BPE - \angle APE$，即$\angle APB = \angle PBD - \angle PAC$。