12. 化简:
(1)$\pm\sqrt{289}$;
(2)$-\sqrt{0.0256}$;
(3)$\sqrt{\frac{169}{196}}$;
(4)$\sqrt{(-8)^{2}}$.
(1)$\pm\sqrt{289}$;
(2)$-\sqrt{0.0256}$;
(3)$\sqrt{\frac{169}{196}}$;
(4)$\sqrt{(-8)^{2}}$.
答案:
【解析】:
本题主要考查平方根的定义及性质,算术平方根的定义及其性质。
(1) 对于 $\pm\sqrt{289}$,需要找到一个数,其平方等于289。
因为 $17^2 = 289$,所以 $\pm\sqrt{289} = \pm 17$。
(2) 对于 $-\sqrt{0.0256}$,需要找到一个数,其平方等于0.0256,然后取其负的平方根。
因为 $0.16^2 = 0.0256$,所以 $-\sqrt{0.0256} = -0.16$。
(3) 对于 $\sqrt{\frac{169}{196}}$,需要找到一个分数,其平方等于 $\frac{169}{196}$。
因为 $\left(\frac{13}{14}\right)^2 = \frac{169}{196}$,
所以 $\sqrt{\frac{169}{196}} = \frac{13}{14}$。
(4) 对于 $\sqrt{(-8)^{2}}$,首先计算 $(-8)^{2} = 64$,然后找到一个数,其平方等于64。
因为 $8^2 = 64$,所以 $\sqrt{(-8)^{2}} = 8$。
【答案】:
(1) $\pm 17$
(2) $-0.16$
(3) $\frac{13}{14}$
(4) $8$
本题主要考查平方根的定义及性质,算术平方根的定义及其性质。
(1) 对于 $\pm\sqrt{289}$,需要找到一个数,其平方等于289。
因为 $17^2 = 289$,所以 $\pm\sqrt{289} = \pm 17$。
(2) 对于 $-\sqrt{0.0256}$,需要找到一个数,其平方等于0.0256,然后取其负的平方根。
因为 $0.16^2 = 0.0256$,所以 $-\sqrt{0.0256} = -0.16$。
(3) 对于 $\sqrt{\frac{169}{196}}$,需要找到一个分数,其平方等于 $\frac{169}{196}$。
因为 $\left(\frac{13}{14}\right)^2 = \frac{169}{196}$,
所以 $\sqrt{\frac{169}{196}} = \frac{13}{14}$。
(4) 对于 $\sqrt{(-8)^{2}}$,首先计算 $(-8)^{2} = 64$,然后找到一个数,其平方等于64。
因为 $8^2 = 64$,所以 $\sqrt{(-8)^{2}} = 8$。
【答案】:
(1) $\pm 17$
(2) $-0.16$
(3) $\frac{13}{14}$
(4) $8$
13. 求下列各式中$x$的值.
(1)$4x^{2}-49= 0$;
(2)$(x+2)^{2}= 25$.
(1)$4x^{2}-49= 0$;
(2)$(x+2)^{2}= 25$.
答案:
【解析】:
(1) 对于方程 $4x^{2} - 49 = 0$,首先移项得到 $4x^{2} = 49$,然后两边同时除以4,得到 $x^{2} = \frac{49}{4}$,最后利用平方根的定义,得到 $x = \pm \sqrt{\frac{49}{4}} = \pm \frac{7}{2}$。
(2) 对于方程 $(x + 2)^{2} = 25$,直接利用平方根的定义,得到 $x + 2 = \pm 5$,然后分别求解两个一元一次方程,得到 $x = 5 - 2 = 3$ 或 $x = -5 - 2 = -7$。
【答案】:
(1) $x = \pm \frac{7}{2}$
(2) $x = 3$ 或 $x = -7$
(1) 对于方程 $4x^{2} - 49 = 0$,首先移项得到 $4x^{2} = 49$,然后两边同时除以4,得到 $x^{2} = \frac{49}{4}$,最后利用平方根的定义,得到 $x = \pm \sqrt{\frac{49}{4}} = \pm \frac{7}{2}$。
(2) 对于方程 $(x + 2)^{2} = 25$,直接利用平方根的定义,得到 $x + 2 = \pm 5$,然后分别求解两个一元一次方程,得到 $x = 5 - 2 = 3$ 或 $x = -5 - 2 = -7$。
【答案】:
(1) $x = \pm \frac{7}{2}$
(2) $x = 3$ 或 $x = -7$
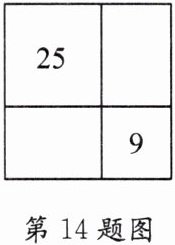
14. 已知一个大正方形内的两个小正方形,面积如图所示,求大正方形的面积.

答案:
解:由图可知,两个小正方形的面积分别为25和9。
则它们的边长分别为$\sqrt{25}=5$和$\sqrt{9}=3$。
观察图形,大正方形的边长为两个小正方形边长之和,即$5 + 3 = 8$。
所以大正方形的面积为$8^2 = 64$。
答:大正方形的面积为64。
则它们的边长分别为$\sqrt{25}=5$和$\sqrt{9}=3$。
观察图形,大正方形的边长为两个小正方形边长之和,即$5 + 3 = 8$。
所以大正方形的面积为$8^2 = 64$。
答:大正方形的面积为64。
思维与拓展1
已知$0<x<1$,且$x+\frac{1}{x}= \sqrt{7}$,求$x-\frac{1}{x}$的值.
已知$0<x<1$,且$x+\frac{1}{x}= \sqrt{7}$,求$x-\frac{1}{x}$的值.
答案:
【分析】:
本题主要考查二次根式的化简以及完全平方公式的运用。
首先,我们知道$x+\frac{1}{x}=\sqrt{7}$,需要对等式两边同时平方,然后利用平方差公式以及已知条件$0<x<1$来求解$x-\frac{1}{x}$。
【解答】:
对等式$x+\frac{1}{x}=\sqrt{7}$两边同时平方,得到
$(x+\frac{1}{x})^2=7$
根据平方差公式展开左边,得到
$x^2+2+\frac{1}{x^2}=7$
即$x^2+\frac{1}{x^2}=5$
考虑$(x-\frac{1}{x})^2$,根据平方差公式,它可以表示为
$(x-\frac{1}{x})^2 = x^2 - 2 + \frac{1}{x^2}$
将$x^2+\frac{1}{x^2}=5$代入上式,得到
$(x-\frac{1}{x})^2 = 5 - 2 = 3$
由于$0<x<1$,所以$x$是正数且小于1,而$\frac{1}{x}$是$x$的倒数,必然大于1,因此$x-\frac{1}{x}$必然是负数。
所以,对$(x-\frac{1}{x})^2=3$开方,并取负值,得到
$x-\frac{1}{x}=-\sqrt{3}$
【答案】:
$-\sqrt{3}$
本题主要考查二次根式的化简以及完全平方公式的运用。
首先,我们知道$x+\frac{1}{x}=\sqrt{7}$,需要对等式两边同时平方,然后利用平方差公式以及已知条件$0<x<1$来求解$x-\frac{1}{x}$。
【解答】:
对等式$x+\frac{1}{x}=\sqrt{7}$两边同时平方,得到
$(x+\frac{1}{x})^2=7$
根据平方差公式展开左边,得到
$x^2+2+\frac{1}{x^2}=7$
即$x^2+\frac{1}{x^2}=5$
考虑$(x-\frac{1}{x})^2$,根据平方差公式,它可以表示为
$(x-\frac{1}{x})^2 = x^2 - 2 + \frac{1}{x^2}$
将$x^2+\frac{1}{x^2}=5$代入上式,得到
$(x-\frac{1}{x})^2 = 5 - 2 = 3$
由于$0<x<1$,所以$x$是正数且小于1,而$\frac{1}{x}$是$x$的倒数,必然大于1,因此$x-\frac{1}{x}$必然是负数。
所以,对$(x-\frac{1}{x})^2=3$开方,并取负值,得到
$x-\frac{1}{x}=-\sqrt{3}$
【答案】:
$-\sqrt{3}$
查看更多完整答案,请扫码查看


